De vuelta a lo básico (Parte 2)

Introducción

En mi artículo anterior, comenté que comenzaría una “serie” de artículos explicando conceptos básicos, para democratizar y clarificar el conocimiento respecto a temas recientes, en particular la IA, que está causando revuelo y hay mucho sensacionalismo en los medios y redes sociales. Algunos ejemplos:

• Inteligencia Artificial Desarrolló su Propio Idioma
• Inteligencia Artificial Cobró Conciencia Propia

Otros ejemplos hay muchos y no puedo ponerlos por espacio; hay variados posts en LinkedIn también sembrando desinformación y hasta miedos en algunas personas.

Como expliqué en mi artículo Generando Imágenes con VQ-VAE, la generación de imágenes es el simple proceso de encontrar una distribución de probabilidad $p(x)$, tal que al muestrear de dicha distribución podemos generar una imagen nueva, que no fue vista por el modelo en su fase de entrenamiento (este entrenamiento consiste en proveer al modelo un conjunto de imágenes para estimar $p(x)$).

Si quieres entender lo básico de probabilidad, te invito a leer mi artículo De Vuelta a lo Básico, donde explico de manera muy sencilla y resumida algunos índices estadísticos y una breve introducción a qué es la probabilidad.

Cuando mencioné $p(x)$, $x$ es una variable aleatoria que representa una imagen en el caso de VQ-VAE. En este artículo, explico en qué consisten las variables aleatorias y una que otra curiosidad sobre estadística y probabilidad.

Variables Aleatorias

Dado un experimento y su correspondiente conjunto de resultados posibles (espacio muestral), una variable aleatoria asoocia un número particular a cada resultado, el cual llamamos valor de la variable aleatoria. Matemáticamente, una variable aleatoria es una función que mapea el resultado de un experimento a un valor real.

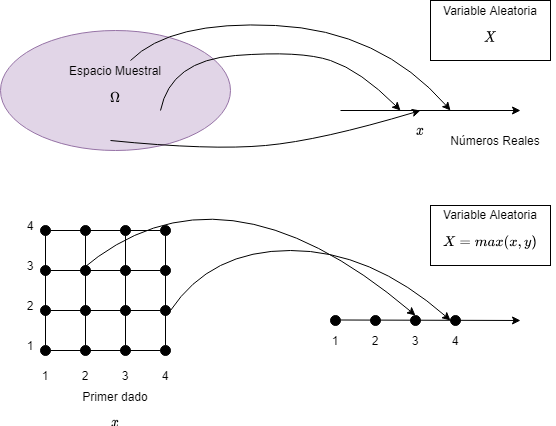
Fig 1: Variable aleatoria discreta.

En la figura se muestra un ejemplo de variable aleatoria. Por ejemplo si se tiene el experimento de lanzar dos dados de 4 caras, donde los lanzamientos los representamos como los pares $(x, y)$, entonces se podría definir como variable aleatoria $X = max(x, y)$, por ejemplo en el caso en que el resultado del experimento sea $(4, 1)$, entonces la variable $X$ tomaría el valor 4.

Otro ejemplo, en un experimento que involucre una secuencia de 5 lanzamientos de una moneda, el número de caras en la secuencia podría ser una variable aleatoria. La secuencia en sí (ej. HHTHT) no es una variable aleatoria, ya que no tiene un valor numérico explícito.

Conceptos principales relacionados a Variables Aleatorias

Considerando un modelo probabilístico de un experimento:

• Una variable aleatoria es una función con valores reales de los resultados de un experimento.
• Una función de una variable aleatoria define otra variable aleatoria.
• Podemos asociar a cada variable aleatoria ciertas “tendencias” de interés, por ejemplo el promedio y la varianza.
• Una variable aleatoria puede estar condicionada por un evento o por otra variable aleatoria.
• Existe una noción de independencia de una variable aleatoria con respecto a un evento u otra variable aleatoria.

Una variable aleatoria, se dice que es discreta, si su rango (el conjunto de valores que puede tomar) es finito o infinito contable (por ejemplo, los números naturales son contables, pues puedo enumerarlos, sin embargo los números realos no porque ¿qué número viene después del 0?). En los ejemplos anteriores, los valores que pueden tomar las variables definidas son limitados: en el caso de la secuencia de 5 lanzamientos de moneda, la variable cantidad de caras, puede tomar los valores 0, 1, 2, 3, 4, 5. En el caso del lanzamiento de los dos dados y la variable max(x, y), esta puede tomar los valores 1, 2, 3, 4, 5, 6.

La forma más importante de caracterizar una variable aleatoria, es a través de las probabilidades de los valores que puede tomar. Para una variable discreta $X$, estos valores se capturan con la función masa de probabilidad de $X$, denotada como $p_X$. En particular, si $x$ es un número real, la probabilidad de masa de $x$, denotada como $p_X(x)$, es la probabilidad del evento $\left\{X = x\right\}$ que consiste en todos los resultados llevan a la variable $X$ tomar el valor $x$:

$$p_X(x) = P\left(\left\{X = x\right\}\right)$$

Consideremos el ejemplo de lanzar dos monedas, y consideremos $X$ como la cantidad de caras obtenidas. Observamos que la variable puede tomar los valores $0, 1, 2$, luego la distribución de masa de probabilidad de $X$ es:

$$ p_X(x)= \left\{ \begin{array}{ll} 1/4 & \mbox{si } x = 0 \text{ o } x = 2 \\ 1/2 & \mbox{si } x = 1 \\ 0 & \mbox{en cualquier otro caso } \end{array} \right.$$

Como ejercicio para el lector, pueden calcular la función de masa de probabilidad para el experimento del lanzamiento de dos dados con $X = max(x, y)$.

Se debe notar que se cumple:

$$\sum_{x} p_X(x) = 1$$

Donde en la suma anterior, $x$ puede tomar todos los posibles valores de $X$. Esto es una consecuencia de los axiomas de aditividad y normalización.

Un ejemplo importante de variable aleatoria, es la variable aleatoria de Bernoulli. Esta variable considera el lanzamiento de una moneda, cuya probabilidad de cara es $p$, y cruz $1 - p$. Esta variable toma dos valores, 1 o 0, dependiendo del resultado del lanzamiento. La distribución de probabilidad de masa es:

$$ p_X(x)= \left\{ \begin{array}{ll} p & \mbox{si } x = 1 \\ 1 - p & \mbox{si } x = 0 \\ \end{array} \right. $$

Pese a su simplicidad, la variable de Bernoulli es muy importante. En la práctica, se utiliza para modelar situaciones probabilísticas con dos posibles resultados, por ejemplo:

• Cliente compra o no compra producto o servicio.
• El estado de un teléfono en un tiempo dado es disponible u ocupado.
• La preferencia de una persona puede ser a favor o en contra de un candidato político.

Otros ejemplos de variables aleatorias típicas usadas son: Binomial, Geométrica y de Poisson.

Esperanza y varianza de una variable aleatoria

Usualmente es deseable, resumir la información de una variable aleatoria en una sola magnitud, en lugar de varios números asociados a las probabilidades de los valores posibles de la variable. Esto se logra mediante la esperanza de $X$, que es un promedio ponderado (a través de probabilidades) de los posibles valores de $X$.

$$E[X] = \sum_x {xp_X(x)} $$

Una intuición de esta medida es pensar en la esperanza de una variable aleatoria como el centro de gravedad o centro de masa de la función de probabilidad de masa.

Otra medida importante asociada a una variable aleatoria $X$ es la varianza de $X$, que se define como la esperanza de la variable aleatoria $(X - E[X])^2$, es decir:

$$var(X) = E\left[(X - E[X])^2\right]$$

La interpretación es la misma que vimos en la semana 1, a diferencia que ahora conocemos el modelo probabilístico de la variable aleatoria.

Es bastante común que existan variables aleatorias con un rango continuo de posibles valores, algunos ejemplos: velocidad de un vehículo en una carretera, estatura de un grupo de interés, etc. Además, las variables continuas permiten usar un conjunto de herramientas de cálculo que usualmente permiten análisis que no son posibles de realizar en un modelo discreto. Finalmente, todos los conceptos y métodos vistos sobre variables aleatorias discretas tienen una contraparte continua.

Una variable $X$ se dice que es continua si existe una función no negativa $f_X$, llamada función de densidad de probabilidad de $X$, tal que:

$$P(X \in B) = \int_B {f_X(x)dx}$$

y que puede ser interpretada como el área bajo la curva del gráfico de la función de densidad de probabilidad. Por otro lado, la función $f_X(x) \geq 0$ para todo $x$ y $\int_{-\infty}^{\infty} {f_X(x)dx} = 1$ (axioma de normalización). También se pueden definir las medidas de esperanza y varianza en una variable continua $X$:

$$E[X] = \int_{-\infty}^{\infty} {xf_X(x)dx}$$

$$var(X) = E\left[(X - E[X])^2\right] = \int_{-\infty}^{\infty} {\left(x - E[x]\right)^2f_X(x)dx}$$

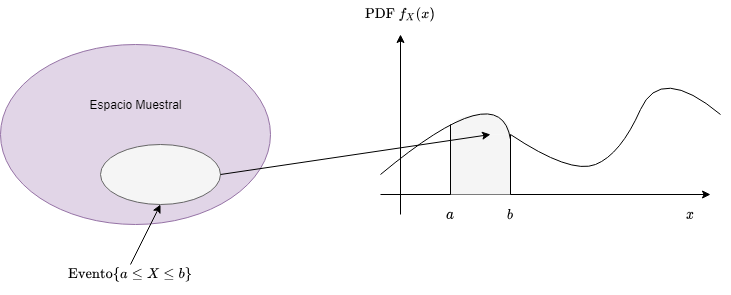
Fig 2: Variable aleatoria continua.

Observación: No es necesario saberse de memoria las fórmulas o saber resolver integrales, etc. Lo importante es tener la intuición de qué significa una variable aleatoria continua y su función de densidad de probabilidad. En particular, es importante entender que el área bajo la curva de esta función debe ser 1 (axioma de normalización), y que una porción de esa área, representa la probabilidad de que un determinado evento ocurra. Por ejemplo, si se modela la estatura, como una variable aleatoria continua, no tendría sentido intentar calcular la probabilidad de que una persona tenga estatura 1.653... (sería 0), lo que interesa es cuál es la probabilidad de encontrar personas entre un determinado rango de estaturas, y en este segundo caso, la noción de área bajo la curva sirve para tener una idea más clara del problema.

Un ejemplo bastante usado de variable aleatoria continua son las variables aleatorias normales. Una variable aleatoria $X$ se dice que es normal o Gaussiana si tiene una función de densidad de probabilidad de la forma:

$$f_X(x) = \frac{1}{\sqrt{2 \pi \sigma}} e^{-(x - \mu)^2/2\sigma^2}$$

La esperanza y la varianza de X se pueden calcular, encontrándose que: $E[X] = \mu$ y $var(X) = \sigma^2$. En general, se dice que la distribución normal está parametrizada por $\mu$ y por $\sigma^2$. Un caso particular de la variable aleatoria normal es la variable aleatoria normal estandarizada, en el que $\mu = 0$ y $var(X) = 1$. Este tipo de variable se usa frecuente mente en procesamiento de señales, u en otros fenómenos donde se quiere modelar el ruido de una señal.

Visualización de variables

Histogramas

Un histograma nos entrega una interpretación visual de datos numéricos, indicando el número de observaciones que poseen valores en un determinado rango. Estos rangos de valores se conocen como clases o bins. La frecuencia de datos que caen en cada bin se ilustra mediante una barra vertical. Mientras más alta sea la barra, mayor es la cantidad de datos de un bin. Una aplicación bastante usada es determinar si una variable “se parece” o puede aproximarse a una variable normal, para ello lo que se hace es normalizar el histograma (axioma de normalización)dividiendo por total_obs*ancho_bin. A continuación se muestran algunos ejemplos.

El conjunto de datos que utilizaré es Quality of Gobernment, ya que este material es viejo, tengo una versión menos actualizada, pero puede observarse que el .csv es descargable:

import pandas as pd


df = pd.read_csv("qog_std_cs_jan18.csv")
df.head()

Graficamos histograma, hay varias formas de hacerlo, por ahora lo haremos con la biblioteca seaborn:

%matplotlib inline

import seaborn as sns

# United nations development program (Human development index)
undp_hdi_notna = df["undp_hdi"].dropna()

sns.distplot(undp_hdi_notna, bins=20, kde=False)

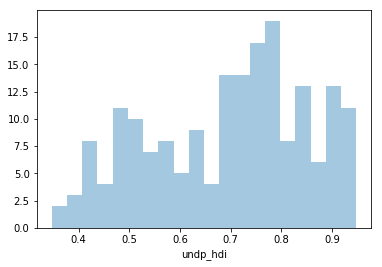
Fig 3: Ejemplo de histograma.

Veamos qué tanto se acerca la distribución de los datos a una distribución normal. Para ello normalizamos el histograma, y graficamos la función de densidad de probabilidad de una variable aleatoria normal. Podemos usar como aproximación el promedio y la desviación estándar de la muestra. La función de densidad de probabilidad normal viene implementada en la biblioteca scipy.

from scipy.stats import norm
import numpy as np
import matplotlib.pyplot as plt

x = np.linspace(0, 1.4, 100)

sns.distplot(undp_hdi_notna, bins=20, kde=False, norm_hist=True)

# Graficar histograma normalizado (como función de densidad de probabilidad)
# Se normaliza para cumplir el axioma de normalización, esto se logra
# Dividiendo el conteo de cada bin por la cantidad de muestras*largo_bin
plt.plot(x, norm.pdf(x, undp_hdi_notna.mean(), undp_hdi_notna.std()), "r")

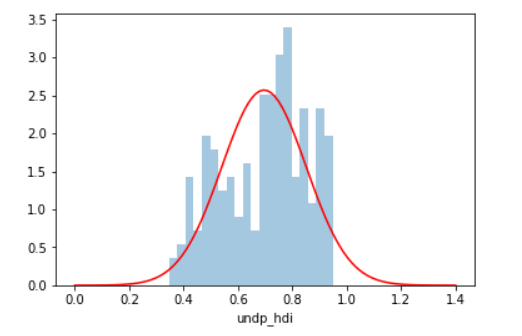
Fig 3: Ejemplo de histograma con gaussiana superpuesta.

Es interesante también explorar un poco más la variable aleatoria normal. Veamos qué ocurre al variar los parámetros de la media y la desviación estándar. También grafiquemos la función acumulada de densidad (que en el infinito debe ser igual a 1, ya que es el área bajo la curva de la función de densidad de probabilidad):

x = np.linspace(-10, 10, num=500)

# Gráficos
fig, (ax1, ax2) = plt.subplots(1, 2, figsize=(15, 7))
fig.suptitle(r"Distribuciones normales para distintos valores de $\mu$ y $\sigma$")
ax1.plot(x, norm.pdf(x, 0, 1), "r")
ax1.plot(x, norm.pdf(x, -1, 2), "g")
ax1.plot(x, norm.pdf(x, 2, 5), "b")
ax1.legend((r"$\mu = 0, \sigma = 1$", r"$\mu = -1, \sigma = 2$", r"$\mu = 2, \sigma = 5$"))
ax2.plot(x, norm.cdf(x, 0, 1), "r")
ax2.plot(x, norm.cdf(x, -1, 2), "g")
ax2.plot(x, norm.cdf(x, 2, 4), "b")
ax2.legend((r"$\mu = 0, \sigma = 1$", r"$\mu = -1, \sigma = 2$", r"$\mu = 2, \sigma = 5$"))

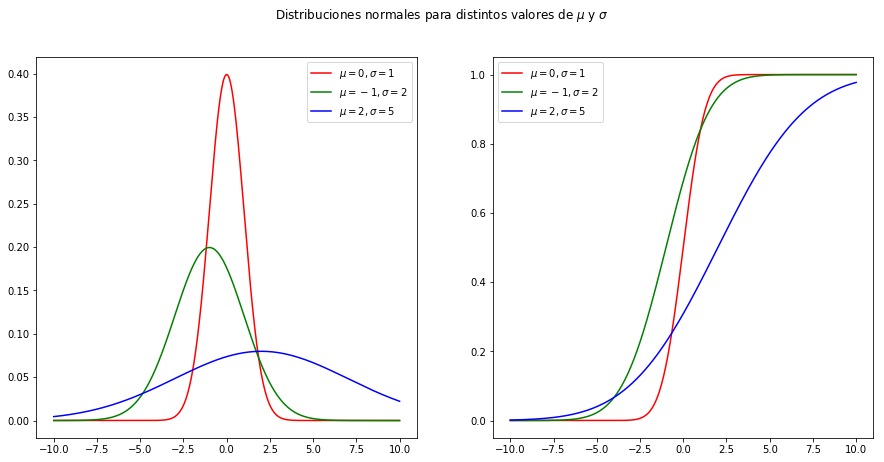
Fig 4: Ejemplo de distribución Gaussiana con diferentes parámetros para $\mu$ y $\sigma$.

Teoremas de Límites

No iremos con la matemática dura de esto, sólo con la intuición, pero notando que de todas formas, una vez digerida la intuición es bueno intentar entender la matemática detrás de los teoremas. Supongamos que tenemos una secuencia $X_1, X_2, \ldots$ de variables aleatorias independientes e idénticamente distribuidas (i.i.d) con promedio $\mu$ y varianza $\sigma^2$. Consideremos la variable $S_n$:

$$S_n = X_1 + X_2 + \ldots + X_n$$

como la suma de las primeras $n$ variables. Los teoremas de límites se enfocan en establecer propiedades para $S_n$ y variables aleatorias relacionadas a medida que $n$ aumenta. Como establecimos que las variables eran independientes, se tiene:

$$var(S_n) = var(X_1) + var(X_2) + \ldots + var(X_n) = n\sigma^2$$

Por lo tanto, la dispersión de la distribución $S_n$ aumenta a medida que $n$ aumenta, y no puede tener un límite que signifique algo. Por otro lado, la situación es diferente si consideramos el $promedio de la muestra$:

$$M_n = \frac{X_1 + \ldots + X_n}{n} = \frac{S_n}{n}$$

Si calculamos las propiedades de $M_n$, llegamos a:

$$E[M_n] = \mu, \quad var(M_n) = \frac{\sigma^2}{n}$$

En particular, la varianza de $M_n$ tiende a 0 a medida que $n$ aumenta, y la esperanza de la distribución de $M_n$ debe ser muy cercana al promedio $\mu$. Estos hechos, nos entregan una intuición para la interpretación de que la esperanza $E[X] = \mu$ es equivalente al promedio de una larga cantidad de muestras independientes sacadas de la distribución de $X$.

Por otro lado, también podemos considerar una cantidad que es un punto medio entre $M_n$ y $S_n$. Podemos restar $n\mu$ de $S_n$, para obtener una variable aleatoria con promedio 0 ($S_n - n\mu$) y dividir por $\sigma\sqrt{n}$, para formar la siguiente variable aleatoria:

$$Z_n = \frac{S_n - n\mu}{\sigma\sqrt{n}}$$

Puede observarse que:

$$E[Z_n] = 0, \quad var(Z_n) = 1$$

Ya que la varianza y la esperanza de $Z_n$ se mantienen constantes a medida que $n$ aumenta, la distribución de $Z_n$ no se agranda ni se achica. El teorema del límite central está relacionado con la forma asintótica de la distribución de $Z_n$ y asegura que dicha distribución se convierte en la distribución norma estándar.

Para probar empíricamente las intuiciones entregadas hasta ahora, podemos usar el mismo conjunto de datos previo. En este ejemplo exploraremos la columna gle_cgdpc (PIB per cápita):

%matplotlib inline

import matplotlib.pyplot as plt
import numpy as np
import pandas as pd


from scipy.stats import norm


df = pd.read_csv("semana3/apoyo/qog_std_cs_jan18.csv")

# Calcular valores "verdaderos" de promedio y desv estándar
true_mean = df["gle_cgdpc"].mean()
true_std = df["gle_cgdpc"].std()

# Probar distintos tamaños de muestra
sample_size = [3, 5, 10, 50]

fig, ax = plt.subplots(4, 1, figsize=(15, 20))
fig.suptitle(f"Distribución de media de muestras $\mu = {true_mean}$ y $\sigma = {true_std}$")

experiments = 1000
for k, N in enumerate(sample_size):
    sample_means = np.zeros(experiments)
    for i in range(experiments):
        sample_means[i] = df.sample(N)["gle_cgdpc"].mean()

    ax[k].hist(sample_means, density=True)
    x = np.linspace(np.min(sample_means), np.max(sample_means), num=1000)
    ax[k].plot(x, norm.pdf(x, true_mean, true_std/np.sqrt(N)), "r")
    ax[k].axvline(x=true_mean, color="black", ls="--")
    ax[k].set_title(f"$\overline = {np.mean(sample_means)}$ $\sigma_ = {np.std(sample_means)}$")

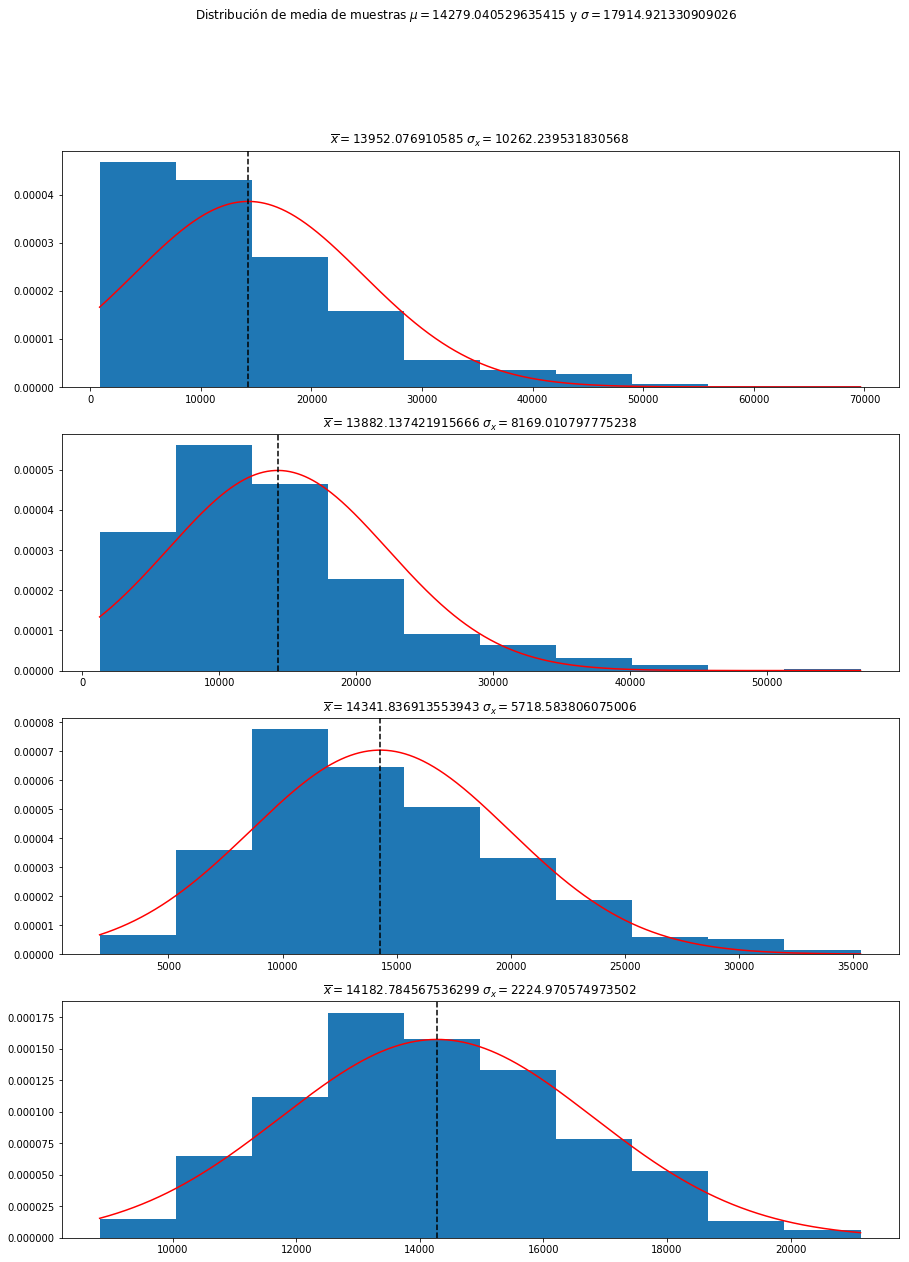
Fig 5: Intuición teorema del límite central.

Básicamente lo que debe observarse, es que a medida que la cantidad de muestras aumenta, el promedio de la distribución comienza a tender al promedio verdadero, y por otro lado, la varianza, disminuye en proporción al tamaño de la muestra.

Reflexiones y datos curiosos

Quiero aclarar que yo no me declaro experto en ninguno de estos temas, consideren esto como mis apuntes y la forma en que yo entiendo la teoría. Puede haber personas que no estén de acuerdo con lo que expongo y supongo que está bien.

Como repaso vimos los contenidos de:

• Variables aleatorias
• Variables discretas
• Variables continuas
• Descriptores de las variables aleatorias (Esperanza y Varianza)
• Teorema del límite central

Con esto, espero que entender mis artículos sea más claro, por ejemplo mi artículo Reflexiones y Jugando con Pixeles.

Como datos curiosos:

• La razón por la que por lo general comienzo con aseveraciones polémicas, es para que el artículo sea más llamativo. Me hicieron notar que mi forma de escribir quizás se percibe como muy negativa o tóxica, intentaré trabajar en ello.
• Nunca apliqué realmente a un doctorado (PhD), intenté algunos, pero no estaba listo en ese tiempo. Por otro lado, cuando terminé mi MSc. tenía una deuda muy grande con el banco (para financiar mis estudios de pre-grado), así que prioricé pagar esa deuda y vivir tranquilo. Quizás en un tiempo más intentaré postular nuevamente
• Espero que la gente logre comprender que GenAI y AI no es magia, y que todo tiene una explicación. Creo que el problema abierto e interesante es entender por qué la arquitectura de Transformers funciona tan bien.
• Probablemente en algún artículo más adelante clarifique cómo funciona GPT (aunque primero tengo que estudiarlo bien jaja)