De vuelta a lo básico
Introducción
Estuve revisando material de cuando hacía clases/ayudantías en diversos lugares (que me reservaré ya que no es información relevante), y noté que si bien viven en sitios olvidados, podría revivir dicho material. Por otro lado, el material contiene en forma muy resumida algunos temas básicos de estadística y probabilidad.
En mi más reciente artículo: Generando Imágenes con VQ-VAE, describí la teoría y entregué una implementación básica de una de las arquitecturas fundamentales utilizadas en sistemas de IA generativa (ej. DALL-E). ¿Cómo esto se relaciona con el párrafo anterior? He visto los siguientes perfiles en algunas redes sociales:
- Personas no técnicas (generalmente de marketing) que hablan de IA como si fuesen expertos y peor aún, proliferan información incorrecta y sensacionalista.
- Personas técnicas (ej. ingenieros de software) que no tienen buenas bases matemáticas y caen en el mismo juego de lo sensacionalista. En este caso, conectando las
APIde turno, sin tener conocimiento de lo que realmente hacen los sistemas.
Ambos perfiles mencionados, son perjudiciales, ya que llenan las redes sociales con información generalmente errónea y en los peores casos engañosa. Comenté en un sitio, si usted ve a alguien con el encabezado “Generative AI expert” y no encuentra a dicha persona aportando en alguna revista científica en temas de IA, es una mala señal 🚩. Una cosa es ser usuario de una tecnología y otra muy distinta es ser experto en dicha tecnología.
Comenzaré una seria de artículos, en los cuales, de forma muy resumida, intento explicar conceptos fundamentales para entender las tecnologías actuales, con el fin de democratizar la información.
Estadística Descriptiva
Existen 3 descriptores fundamentales de los datos, los cuales se utilizan como estadísticas descriptiva:
- Media
- Mediana
- Desviación estándar
Media
La media de un conjunto de datos discreto es el valor central, específicamente, la suma de los valores dividido por el número de valores.
$$media = \frac{1}{n} \sum_{i=1}^{n} x_i$$
Mediana
La mediana es el valor que separa la mitad inferior y superior de una muestra de datos. La forma de calcularla es, ordenar las muestras. Luego, si se tienen $n$ muestras enúmeradas de $1$ a $n$, es decir $x_1, x_2, \ldots, x_n$, la mediana se calcula como:
$$mediana = \frac{1}{2} \left( x_{\lfloor (n+1)/2\rfloor} + x_{\lceil (n+1)/2\rceil} \right)$$
Supongamos que tenemos las siguientes observaciones de altura $h = (1, 3, 3, 5, 7)$, en este caso la mediana sería $3$, y aplicando la fórmula, se tienen $5$ observaciones, por lo tanto se requiere $0.5 \cdot (x_{3} + x_{3}) = x_{3} = 3$. Ahora supongamos que tenemos las siguientes observaciones $h = (1, 2, 3, 4, 5, 6, 8, 9)$, en este caso el número de observaciones es $8$, número par. Por lo tanto según la fórmula $0.5 \cdot (x_{4} + x_{5}) = 0.5 \cdot (4 + 5) = 4.5$. En el caso par, se consideran las muestras que caen en el medio, y se calcula el punto medio entre ellas. Esto sigue la intuición de la definición de mediana, que es básicamente una medida que separa las observaciones en una mitad inferior y una mitad superior.
Desviación Estándar
La desviación estándar es una medida de cantidad de dispersión en un conjunto de valores. Un valor bajo de desviación estándar muestra que los valores tienden a estar cerca del promedio, mientras que un valor alto indica que los valores tienden a exparcirse en un rango más amplio de valores. Por ejemplo, consideremos dos distribuciones de valores $(50, 50)$, $(0, 100)$. Ambos tienen una media de 50, pero los rangos de valores en la primera no se alejan del promedio, por lo tanto tienen 0 dispersión, mientras que en el segundo caso, la desviación estándar es 50.
$$Desv.Std = \sqrt{\frac{1}{n} \sum_{i=1}^{n} \left( x_i - media \right)^2}$$
Calculo en Python
import math
import numpy as np
import pandas as pd
def mean(array):
return sum(array) / len(array)
def std(array):
avg = mean(array)
return math.sqrt(sum((xi - avg) ** 2 for xi in array) / (len(array)))
def median(array):
sorted_array = sorted(array)
# Indexacion empieza desde 0, por eso le resto 1
n = len(array)
return 0.5 * (
sorted_array[math.floor((n + 1) / 2) - 1]
+ sorted_array[math.ceil((n + 1) / 2) - 1]
)
x1 = [1, 3, 3, 5, 7]
x2 = [1, 2, 3, 4, 5, 6, 8, 9]
print("Usando las formulas y operaciones en python")
print(f"x1; media: {mean(x1)}, mediana: {median(x1)}, desv std: {std(x1)}")
print(f"x2; media: {mean(x2)}, mediana: {median(x2)}, desv std: {std(x2)}")
np_x1 = np.array(x1)
np_x2 = np.array(x2)
print("Usando numpy")
print(
f"x1; media: {np.mean(np_x1)}, mediana: {np.median(np_x1)}, desv std: {np.std(np_x1)}"
)
print(
f"x2; media: {np.mean(np_x2)}, mediana: {np.median(np_x2)}, desv std: {np.std(np_x2)}"
)
df_x1 = pd.DataFrame({"x1": x1})
df_x2 = pd.DataFrame({"x2": x2})
print("Usando pandas")
print(
f"x1; media: {df_x1.x1.mean()}, mediana: {df_x1.x1.median()}, desv std: {df_x1.x1.std()}"
)
print(
f"x1; media: {df_x2.x2.mean()}, mediana: {df_x2.x2.median()}, desv std: {df_x2.x2.std()}"
)
Usando las formulas y operaciones en python
x1; media: 3.8, mediana: 3.0, desv std: 2.039607805437114
x2; media: 4.75, mediana: 4.5, desv std: 2.6339134382131846
Usando numpy
x1; media: 3.8, mediana: 3.0, desv std: 2.039607805437114
x2; media: 4.75, mediana: 4.5, desv std: 2.6339134382131846
Usando pandas
x1; media: 3.8, mediana: 3.0, desv std: 2.280350850198276
x2; media: 4.75, mediana: 4.5, desv std: 2.815771906346718
En pandas la diferencia se debe a que se divide por $n - 1$ en lugar de $n$, para obtener un valor sin sesgo. Queda como tarea para el lector entender lo que es un estimador sesgado y sin sesgo.
Probabilidades y Funciones
Probabilidad
En general, se habla de probabilidad en casos en que existe incertidumbre en una situación. Por ejemplo, si voy al doctor y recibo un tratamiento, ¿Qué tan probable es que con dicho tratamiento me recupere? O por ejemplo, en un casino jugando black jack, ¿Cuál es la probabilidad de que me salga black jack en la siguiente mesa?
Un modelo probabilístico es una descripción matemática de una situación incierta. Dicho modelo matemático contiene los siguientes elementos:
- El espacio muestral $\Omega$, que es el conjunto de todos los posibles resultados de un experimento.
- La ley de probabilidad, que asigna a un conjunto $A$ (también llamado evento) de posibiles resultados, un número no negativo $P(A)$ (conocido como la probabilidad de $A$) y que codifica nuestro conocimiento o creencia sobre qué tan posible es que $A$ ocurra.
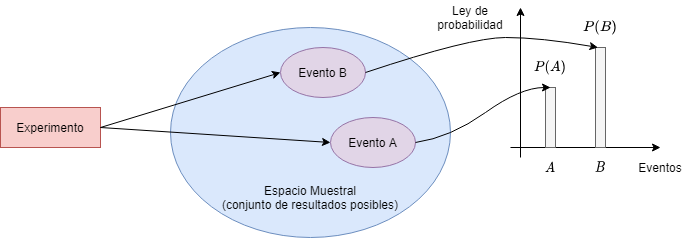
La siguiente figura ilustra los elementos de un modelo probabilístico:

Fig 1: Visualización modelo probabilístico
Todo modelo probabilístico involucra un proceso subyacente, el cual se le denomina experimento, y que producirá exactamente uno de los muchos posibles resultados. El conjunto de todos los posibles resultados se llama espacio muestral del experimento, y se denota $\Omega$. Un subconjunto del espacio muestral, es decir, una colección de posibles resultados, se conoce como evento<.
La ley de probabilidad especifica la “posibilidad” de cualquier resultado, o cualquier conjunto de posibles resultados (evento). Esta ley asigna a cada evento $A$, un número $P(A)$, llamado la probabilidad de $A$, la cual satisface los siguientes axiomas:
- (No negatividad) $P(A) \geq 0$, para todo evento $A$
- (Aditividad) Si $A$ y $B$ son dos eventos disjuntos, entonces la probabilidad de su union satisface:
$$P(A \cup B) = P(A) + P(B)$$
Esto se puede generalizar a la union de más eventos.
- (Normalización) La probabilidad del espacio muestral $\Omega$ es igual a 1, es decir $P(\Omega) = 1$
Consideremos el experimento de lanzar dos dados de 4 caras. Asumimos que los dados no están cargados, y con este supuesto queremos decir que cada uno de los 16 posibles resultados: $\{(i, j) | i, j = 1, 2, 3, 4\}$ cada uno tiene la misma probabilidad de ocurrir $\frac{1}{16}$. Algunos ejemplos:
- $P(\{ \text{la suma de los dados es par}\}) = \frac{8}{16} = \frac{1}{2}$
- $P(\{ \text{la suma de los dados es impar}\}) = \frac{8}{16} = \frac{1}{2}$
- $P(\{ \text{El primer dado es igual al segundo}\}) = \frac{4}{16} = \frac{1}{4}$
- $P(\{ \text{El primer dado es mayor que el segundo}\}) = \frac{6}{16} = \frac{3}{8}$
- $P(\{ \text{Al menos un dado da 4}\}) = \frac{7}{16}$
El espacio muestral y algunos ejemplos de eventos se muestran en la figura 2.
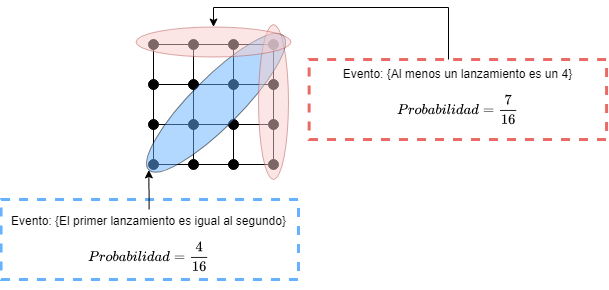
Fig 2: Espacio muestral del experimento de lanzar dos dados de 4 caras.
Probabilidad Condicional
La probabilidad coondicional nos entrega una manera de razonar acerca los resultados de un experimento, basándonos en información parcial.
Algunos ejemplos de situaciones:
- En un experimento de lanzamiento consecutivo de dos dados, nos dicen que la suma es 9. ¿Qué tan posible es que el primer dado haya sido un 6?
- ¿Qué tan probable es que una persona tiene cierta enfermedad dado un test médico que salió negativo?
- Un cliente está usando un la versión gratuita de servicio con cierta frecuencia. ¿Qué tan probable es que acepte una oferta de suscripción premium?
Siendo más precisos, dado un experimento, su espacio muestral correspondiente y su ley de probabilidad, supongamos que el resultado se encuentra dentro de algun evento $B$ dado. Deseamos cuantificar la posibilidad que el resultado pertenece también a otro evento $A$. Por lo tanto, construimos una nueva ley de probabilidad que considera el conocimiento disponible: Una ley de probabilidad que para cualquier evento $A$, especifica la probabilidad condicional de $A$ dado $B$, y se denota como $P\left(A\mid B\right)$
Por otro lado, nos gustaría que las probabilidades condicionales $P\left(A\mid B\right)$ de diferentes eventos $A$, constituyeran una ley de probabilidad que satisfaga todos los axiomas de probabilidad. Este tipo de probabilidades también deben ser consistentes con la intuición en casos especiales, por ejemplo, cuando todos los posibles resultados del experimento son igualmente posibles. Por ejemplo, supongamos que los 6 resultados del lanzamiento de un dado de 6 caras son igualmente probables. Si nos dijeran que el resultado fue par, nos quedan sólo 3 posibles resultados, 2, 4, y 6. Estos resultados en principio tenían la misma probabilidad, por lo tanto ahora que sabemos que el número fue par, debiesen ser igualmente probables. Así, es razonable pensar:
$$P\left(\text{el resultado es 6}\mid \text{el resultado es par}\right) = \frac{1}{3}$$
Generalizando esta intuición, la definición de probabilidad condicional es:
$$P\left(A\mid B\right) = \frac{P(A \cap B)}{P(B)}$$
donde asumimos que $P(B) > 0$; la probabilidad condicional es indefinida si el evento condicionante tiene probabilidad cero.
Dado que $P(A) \geq 0$ y $P(B) > 0$, esta ley de probabilidad satisface el axioma de no negatividad. El axioma de normalización también se satisface:
$$P\left(\Omega \mid B\right) = \frac{P\left( \Omega \cap B\right)}{P(B)} = \frac{P(B)}{P(B)} = 1$$
Y el axioma de aditivdad también se satisface, para cualquier par de eventos disjuntos $A_1$ y $A_2$:
$$ \begin{align} P\left(A_1 \cup A_2 \mid B\right) & = \frac{P\left(\left(A_1 \cup A_2 \right) \cap B\right)}{P(B)}\\ & = \frac{P\left(\left(A_1 \cap B \right) \cup \left(A_2\cap B\right)\right)}{P(B)}\\ & = \frac{P\left(A_1 \cap B \right) + \left(A_2\cap B\right)}{P(B)}\\ & = \frac{P\left(A_1 \cap B \right)}{P(B)} + \frac{\left(A_2\cap B\right)}{P(B)}\\ & = P\left(A_1 \mid B\right) + P\left(A_2 \mid B\right) \end{align} $$
Consideremos nuevamente el experimento de dos lanzamientos de dados de 4 caras, donde los 16 resultados posibles tienen la misma probabilidad. Supongamos que queremos determinar la probabilidad $P\left(A \mid B\right)$ donde:
$$A = \left\{max(X, Y) = m\right\}, \quad B = \left\{min(X, Y) = 2\right\},$$
y $m$ puede tomar cualquiera de los valores 1, 2, 3, 4.
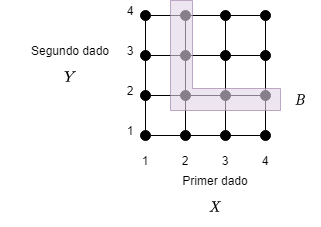
Fig 3: Espacio muestral lanzamiento dos dados.
En la figura 3 se muestra el espacio muestral de un experimento que involucra dos lanzamientos de dados de 4 caras. El evento condicionante $B = \left\{min(X, Y) = 2\right\}$ es el conjunto sombreado en la figura. El evento $A = \left\{max(X, Y) = m\right\}$ comparte con $B$ dos elementos si $m = 3$ o $m = 4$, un elemento si $m = 2$, y ningún elemento si $m = 1$. Por lo tanto tenemos:
$$ P (\left\{max(X, Y) = m\right\} \mid B)= \left\{ \begin{array}{ll} 2/5 & \mbox{si } m = 3 \text{ o } m = 4 \\ 1/5 & \mbox{si } m = 2 \\ 0 & \mbox{si } m = 1 \end{array} \right. $$
Distintos enfoques a la estadística
En el campo de la estadística hay dos prominentes escuelas de pensamiento, con visiones opuestas: la Bayesiana y la clásica ( también llamada frecuentista). Su diferencia fundamental está relacionada con la naturaleza de modelos desconocidos o variables. En una visión Bayesiana, estos modelos se tratan como variables aleatorias (tema que veremos más adelante) con distribuciones conocidas. En la visión clásica, estos modelos/variables se tratan como cantidades determinísticas que se desconocen. En fin, es un tema prácticamente filosófico, pero en términos prácticos, los modelos Bayesianos solían ser intratables computacionalmente, ahora con los avances en computación y en semiconductores (procesadores), muchas investigaciones recientes se enfocan en hacer métodos Bayesianos que puedan ser usados en la práctica. Pueden leer este interesante artículo.
¡Eso es todo amigos!
Por el momento, lo dejaré hasta aquí. Con esta información y definiciones, debiese ser más simple leer mis artículos anteriores. Ya que esto no es un curso ni nada, sólo información básica, sesgada a mi opinión y que se transmite de manera asíncrona, no pondré muchas simulaciones o ejercicios computacionales. Sin embargo, en el futuro puede que agregue algo de código, en caso de ser necesario.
Rezo, para que la gente que está predicando humo, dedique un par de minutos de su vida a entender al menos los fundamentos de lo que predican (actualmente AI y GenAI). En mis otros artículos hablo de varios temas relacionados; armando el puzle completo, se puede entender mejor cómo funcionan las tecnologías actuales.
¡Abrazos!