Explicando las Máquinas de Soporte Vectorial
Esta entrada intentaré explicar en términos simples en qué consisten máquinas de soporte vectorial (Support Vector Machines o SVM), dando detalles y mostrando ejemplos, pros y contras. También, preguntas para reflexionar al final de la entrada.
Aprovechando la introducción, responderé un par de preguntas que me llegan recurrentemente, espero poder ayudar:
- ¿Cómo aprendiste sobre IA y ML?
- ¿Cómo te has movido en tantos roles (e.g. Data Engineering, Backend)?
- ¿Seguiste alguna ruta en particular?
Las respuestas están al final de esta entrada.
Máquinas de Soporte Vectorial
Primero se debe entender qué problema intentan resolver las máquinas de soporte vectorial. Volvamos a lo básico: en un problema de clasificación se tiene una función $h: \mathbb{R} \longrightarrow L$, donde $L$ es un conjunto de etiquetas o clases. En particular, en clasificación binaria se tienen dos clases, y para propósitos de este artículo $L = \{-1, +1\}$.
En general, en los cursos introductorios de Machine Learning se ve revisa como primera unidad el aprendizaje del perceptrón, que en esencia, es una función que buscar un hiperplano que particione el espacio vectorial y separe las clases positivas de las negativas. Cuando es posible hacer esto, se habla de separabilidad lineal. En la figura 1, se muestra una animación del aprendizaje del perceptrón.

Fig 1: Aprendizaje del perceptrón en un conjunto de datos separable linealmente
El lector atento, podrá notar que pueden existir infinitos hiperplanos que logren particionar un espacio logrando separar las clases. Sin embargo, debe existir un hiperplano que sea “mejor” que el resto bajo algún criterio. De aquí sale el concepto de margen. El margen es en esencia, la distancia de separación entre el hiperplano y los puntos más cercanos al hiperplano (por cada clase). Intuitivamente, el “mejor” hiperplano, podría ser el que maximice este margen, ya que estaría logrando la máxima separación lineal entre las clases. Las máquinas de soporte vectorial intentan encontrar este hiperplano.

Fig 2: Conjunto de datos separable linealmente ¿Cuál es el méjor hiperplano?
Intuición y entrenando un modelo SVM
Supongamos que tenemos un punto $x \in \mathbb{R}$. Consideremos la función:
$$f: \mathbb{R}^n \longrightarrow \mathbb{R}$$
$$x \longrightarrow \langle w, x \rangle + b$$
Donde $w$ y $b$ son parámetros de $f$. El hiperplano que separa ambas clases en el problema de clasificación binaria está dado por:
$$\{ x \in \mathbb{R}: f(x) = 0\}$$
Para calcular la clase a la que pertenece un dato nuevo $x_{test}$, se calcular el valor $f(x_{test})$ y se clasifica, por ejemplo con la clase $+1$ si $f(x_{test}) \geq 0$ o $-1$ en caso contrario.
Al momento de entrenar, se requiere que los ejemplos de la clase positiva se encuentren en el lado positivo del hiperplano, $\langle w, x_n \rangle + b \geq 0$ cuando $y_n = +1 $ y la clase negativa en el otro lado $\langle w, x_n \rangle + b < 0$ cuando $y_n = -1$ Generalmente se utiliza la función signo para escribir de forma compact esto, es decir: $y_n = sign(\langle w, x_n \rangle + b)$
Margen y problema de optimización
Supongamos que el punto $x_a$ es el punto más cercano al hiperplano $\langle w, x_a \rangle + b > 0$ ($w$ es un vector ortogonal al hiperplano). Consideremos también una escala, tal que $\langle w, x_a \rangle + b = 1$, la razón es que si consideramos la escala en la que están los datos (escala de $x_n$), si cambiamos la unidad de medida o valores de $x$ (por ejemplo $10x_n$), la distancia al hiperplano también va a cambiar. Consideremos una escala tal que $\langle w, x_a \rangle + b = 1$.

Fig 3: Intuición margen máximo
Como se muestra en la figura 3, la proyección $x_a’$ de $x_a$ en el plano, está dada por:
$$x_a = x_a’ - \displaystyle r \frac{w}{||w||}$$
Donde $r$ es la distancia al hiperplano y consideramos la dirección del vector $w$. Ya que $x_a’$ se encuentra en el hiperplano, entonces $\langle w, x_a’ \rangle + b = 0$, si resolvemos:
$$ \langle w, x_a - \displaystyle r \frac{w}{||w||} \rangle + b = 0$$
$$\langle w, x_a\rangle + b - \langle w, \displaystyle r \frac{w}{||w||} \rangle = 0$$
$$1 - r\displaystyle \frac{w^Tw}{||w||} = 1 - r\displaystyle \frac{||w||^2}{||w||} = 0$$
$$r = \displaystyle \frac{1}{||w||}$$
En esencia, para maximizar el margen $r$, debemos maximizar $\displaystyle \frac{1}{||w||}$, esto sería equivalente a minimizar $||w||$, luego:
$$
\begin{aligned}
\min_{w,b} \quad & \frac{1}{2}||w||^2 \\
\textrm{s.t.} \quad & y_n (\langle w, x_n \rangle + b) \geq 1\\
\end{aligned}
$$
Donde $\frac{1}{2}||w||^2$ no cambia al valor optimo de $w$, se escribe sólo por conveniencia (al calcuar la derivada parcial con respecto a $w$ para encontrar el óptimo, queda más simple de analizar), y las restricciones están relacionadas al ajuste de datos.
Este problema de optimización se resuelve con programación cuadrática. La forma estándar que consideran como entrada los algoritmos de programación cuadrática, es la siguiente:
$$ \begin{aligned} \min_{x} \quad & \frac{1}{2} x^TPx + q^Tx\\\ \textrm{s.t.} \quad & Gx \leq h\\ & Ax = b \end{aligned} $$
Utilizando la biblioteca cvxopt en python, y escribiendo el programa en la forma estándar, tenemos el siguiente código en Python (asumiendo que $x$ tiene dos dimensiones)
from cvxopt import matrix, solvers
P = matrix(np.eye(3))
q = matrix(np.zeros((3, 1)))
G = matrix(-y * np.concatenate([np.ones((len(y), 1)), x], axis=1))
h = matrix(-np.ones(len(y)))
sol = solvers.qp(P, q, G, h)
wsol = np.array(sol["x"])
Al graficar la solución, se obtiene:

Fig 4: Hiperplano que optimiza el margen
Interpretación como cáscara convexa
Una interpretación del hiperplano que maximiza el margen, es considerar que cada clase pertence a una cáscara convexa (convex hull). Una cáscara convexa, es básicamente un polígono que cubre los límites de un conjunto de puntos (figura 5).

Fig 5: Cáscara convexa
En esencia, una SVM, maximiza la distancia entre las cáscaras convexas de cada clase.
Margen Duro vs Margen Suave
El problema de optimización previo, asume que las clases son separables linealmente, es decir, la solución no admite soluciones fuera del margen. Esto se conoce como margen duro. Una alternativa, es, en lugar de tener $y_n (\langle w, x_n\rangle) + b \geq 1$, se introduce una variable de flexibilidad $\xi_n$, tal que se permiten ciertos errores de clasificación $y_n (\langle w, x_n\rangle) + b \geq 1 - \xi_n$
$$ \begin{aligned} \min_{w,b,\xi} \quad & \frac{1}{2}w^{T}w+C\sum_{n=1}^{N}{\xi_{n}} \\ \textrm{s.t.} \quad & y_{n}(\langle w, x_{n} \rangle+b)\geq 1 - \xi_{n}\\ &\xi_n\geq0 \\ \end{aligned} $$
Derivación de la forma Dual
El problema de optimización original es maximizar el margen tal que ambas clases son separables. Hasta ahora hemos definido el problema como un problema de minimización. Sin embargo, podemos resolver el problema de optimización utilizando multiplicadores de Lagrange. Tomando la ecuación del margen suave, y utilizando los multiplicadores de lagrange, tenemos:
$$ \begin{aligned} \min_{w,b,\xi, \alpha, \gamma} \quad & \frac{1}{2}w^{T}w \\ & -\sum_{n=1}^{N}\alpha_n(y_{i}(\langle w, x_{n} \rangle+b)+\xi_{i}-1)\\ & -C\sum_{n=1}^{N} \gamma_n\xi_n \\ \end{aligned} $$
Donde $\alpha_n$ y $\gamma_n$ son multiplicadores de Lagrange. Para encontrar el mínimo, debemos calcular gradiente, es decir las derivadas parciales de la función de Lagrange, con respecto a cada variable a optimizar e igualar a cero.
$$ \begin{aligned} \displaystyle \frac{\partial \mathcal{L}}{\partial w} = w^T - \sum_{n=1}^{N} \alpha_n y_n x_n^T = 0 \Rightarrow w = \sum_{n=1}^{N} \alpha_n y_n x_n\\ \displaystyle \frac{\partial \mathcal{L}}{\partial b} = \sum_{n=0}^{N} \alpha_n y_n = 0\\ \displaystyle \frac{\partial \mathcal{L}}{\partial \xi_n} = C - \alpha_n - \gamma_n = 0\\ \end{aligned} $$
Trabajando las ecuaciones y considerando las restricciones, llegamos al siguiente problema de optimización:
$$ \begin{aligned} \min_{\alpha} \quad & \frac{1}{2} \sum_{i=1}^{N}\sum_{j=1}^{N} y_iy_j\alpha_i\alpha_j\langle x_i, x_j\rangle - \sum_{n=1}^{N} \alpha_n \\ \textrm{s.t.} \quad & \sum_{n=1}^{N} \alpha_n y_n = 0 \\ & 0 \leq \alpha_n \leq C \\ \end{aligned} $$
En este caso los vectores $\alpha$ se les conoce vectores de soporte, ya que soportan el margen de máxima separabilidad. De aquí sale el nombre de máquinas de soporte vectorial.
Separabilidad Lineal
Existen casos (me disculpo por el ejemplo clásico) en que no existe un hiperplano que separe ambas clases, como se muestra en la figura 6:

Fig 6: Conjunto de datos no separable linealmente
En este caso, ya que los datos fueron generados en este ejemplo, conocemos el líimite de decisión, el cual está marcado de color negro. Por otro lado, conocemos una transformación $\phi$ tal que $\phi (x) = z$. En la figura 7, se muestra el conjunto de datos transformado al nuevo sistema de coordenadas. Y luego podemos encontrar el máximo margen resolviendo el problema de optimización. El hiperplano se muestra en la figura 7.

Fig 7: Conjunto de datos no separable linealmente en un espacio $z$ donde es separable
El truco del kernel
Supongamos que tenemos un conjunto de datos donde cada registro consiste en dos características $x = (x_1, x_2)$. Lo que podemos hacer es por ejemplo considerar todas las coordenadas posibles (ejemplo: polinomio cuadrado) $z = (x_1, x_2, x_1^2, x_2^2, x_1x_2)$. Si quisieramos agregar más características, este problema se vuelve intratable (ejemplo: 50 características ¿cuántas posibles combinaciones hay para un polinomio cuadrado? ¿y para uno de grado $Q$?).
Si observamos la última derivación del problema de optimización, la solución depende de los vectores de soporte (cantidad de registros) y no de la cantidad de características. En el único momento en que utilizamos las características, es cuando calculamos $\langle x_i, x_j\rangle$. Esto quiere decir, si tuvieramos la función $\phi$, sólo nos interesa el producto interior $\langle \phi(x_i), \phi(x_j)\rangle$. En el caso estándar $\langle x_i, x_j\rangle$ es un kernel lineal. Podemos definir por ejemplo un kernel polinomial:
$$K(x_i, x_j) = (1 + x_i^Tx_j)^D$$
Por ejemplo en la figura 8, se muestra el límite de decisión derivado utilizando un kernel polinomial con $D=2$.
def polynomial_kernel(xi, xj, d):
return (1 + xi.dot(xj))**d
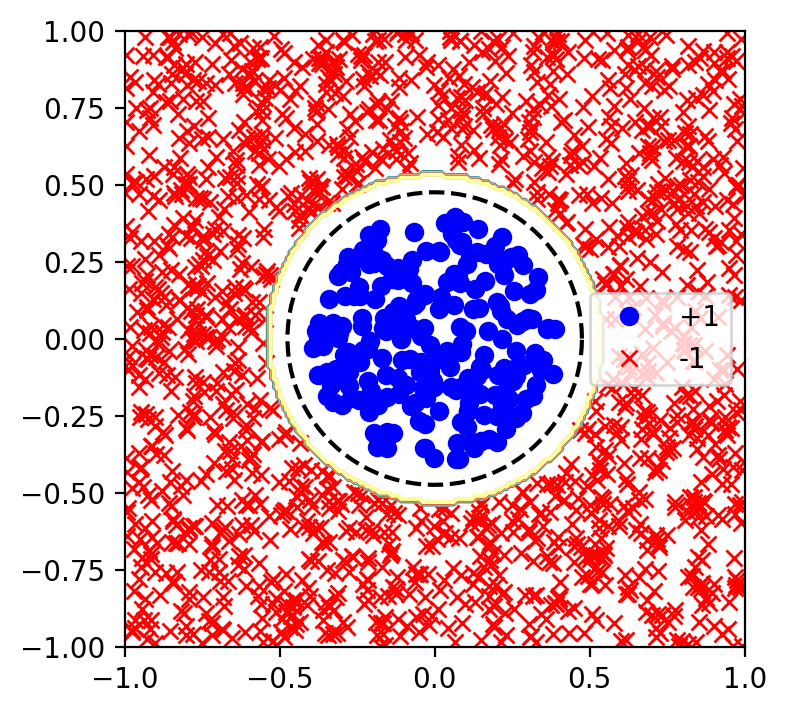
Fig 8: Límite de decisión utilizando kernel polinomial.
Puede notarse que el límite de decisión encontrado es el límite de decisión manualmente generado, con la diferencia que no tuvimos que aplicar directamente la transformación $\phi$ a $x$. La idea de un kernel es en esencia llevar los datos de un espacio a otro espacio de mayor dimensionalidad, donde las clases sean linealmente separables (idealmente).
No todas las funciones son kernel válidos, para que un kernel sea válido, la matriz generada aplicando kernels a todos los pares $x_i$ y $x_j$ debe ser simétrica y semi-definida positiva. Esto quiere decir:
- $K = K^T$
- $\forall \lambda_n, \quad \lambda_n \geq 0$
Donde $\lambda_n$ son los valores propios de $K$ y $K$ es la matriz generada al aplicar el kernel a todos los pares en el conjunto de datos (es decir $K \in \mathbb{R}^{n \times n}$).
Incluso, se pueden encontrar límites de decisión más sofisticados, por ejemplo, consideremos el siguiente conjunto de datos:

Fig 9: Conjunto de datos no separable linealmente.
Podemos utilizar un kernel que utilice una función de base radial (radial basis function o RBF).
def radial_basis_function_kernel(xi, xj, gamma):
return np.exp(-gamma * np.linalg.norm(xi - xj))
Por ejemplo si $C = 1$, se obtiene límite de decisión mostrado en la figura 10.

Fig 10: Límite de decisión con kernel RBF y $C = 1$.
Relajando las restricciones (por ejemplo aumentando $C = 100$), encontramos otro límite de decisión (figura 11).

Fig 10: Límite de decisión con kernel RBF y $C = 100$.
Realizando Predicciones
Para realizar las predicciones, se debe calcular la proyección en el hiperplano:
$$\langle w, \phi(x)\rangle = \sum_{n=1}^{N}\alpha_n y_n K(x, x_n)$$
Y también se debe considerar el hiperplano:
$$b = y_k - \sum_{n=1}^{n} \alpha_n y_n K(x_k, x_n) \quad \text{Any } k, 0 < \alpha_k < C$$
$$y(x) = sign(\langle w, \phi(x)\rangle + b)$$
A continuación se muestra el código en python que implementé hay mucho que optimizar, como por ejemplo:
- Eliminar los $\alpha = 0$ para reducir la cantidad de calculos.
- Calcular $K(x_i, x_j)$ sólo para $\alpha > 0$
Dejo al lector que implemente, como es una implementación de juguete no me preocupé de optimizar.
class SupportVectorMachine:
def __init__(self, C, kernel, *kernel_args):
self._kernel = kernel
self._kernel_args = kernel_args
self.C = C
def train(self, x, y):
n = len(x)
kernel_matrix = np.zeros((n, n))
diag_y = np.diag(y.flatten())
for i in range(n):
for j in range(n):
kernel_matrix[i, j] = self._kernel(
x[i, :], x[j, :], *self._kernel_args)
P = matrix(diag_y.dot(kernel_matrix).dot(diag_y))
q = matrix(-np.ones((len(y), 1)))
G = matrix(np.concatenate([
y.T, -y.T, -np.eye(len(y)), np.eye(len(y))]))
h = matrix(np.concatenate([
np.zeros((len(y) + 2, 1)), self.C*np.ones(y.shape)]))
sol = solvers.qp(P, q, G, h)
alphasol = np.array(sol['x'])
self._alpha = alphasol
k = alphasol.argmax()
xk = x[k, :]
kernel_k = np.zeros((len(x), 1))
for i in range(len(x)):
kernel_k[i] = self._kernel(xk, x[i, :], *self._kernel_args)
self._b = y[k] - (alphasol*y).T.dot(kernel_k)
self._x = x
self._y = y
return self
def predict(self, x_test):
x = self._x
y = self._y
alpha = self._alpha
b = self._b
kernel_new = np.zeros((len(x), len(x_test)))
for i in range(len(x)):
for j in range(len(x_test)):
kernel_new[i, j] = self._kernel(
x_test[j, :], x[i, :], *self._kernel_args)
return np.sign(kernel_new.T.dot(alpha * y) + b)
Conclusiones
- Explicamos la intuición de las SVM y cómo se pueden derivar dos tipos de parámetros, el vector $w$ o los vectores de soporte $\alpha$
- Una interpretación del problema que resuelven las máquinas de soporte vectorial es encontrar la separación máxima entre las cáscaras convexas de los conjuntos para cada clase.
- Un espacio no separable linealmente, se puede separar linealmente en otro espacio dado por una función $\phi$
- La regularización del parámetro $C$ puede suavizar o endurecer las restricciones de margen
- El truco del kernel permite calcular el producto interior de dos vectores en cualquier espacio dimensional, sin necesidad de explícitamente transformar el espacio
- Se pueden diseñar kernels adhoc, siempre que cumplan con las condiciones de Mercer ($K$ es Simetrica y semi-definida positiva)
Para reflexionar:
- Si se puede transformar el espacio dimensional a una dimensión infinita ¿Por qué las máquinas de soporte vectorial no pueden resolver todos los problemas de clasificación?
- Qué desventajas se observan en las máquinas de soporte vectorial? (e.g. escalabilidad, error fuera de muestra)
Respuestas a las preguntas de la introducción
Click para ver mi respuesta
