Reciclando un poquito más de material viejo

Introducción

No es un post tan interesante, pero sigue la temática de reciclar material que alguna vez escribí y que a alguna persona le podrá servir, aunque sea para pasar el ocio.

Reflexiones Iniciales

Algunas personas me han preguntado consejos, como por ejemplo qué cursos tomar, qué hacer para mejorar en X/Y/Z. Aprovecharé de responder, no tengo la menor idea. Supongo que buscando la literatura e intentando estudiar un poco, el espacio de búsqueda se puede reducir.

Aprendizaje No Supervisado

El término aprendizaje no supervisado hace referencia a métodos que extraen información/patrones en los datos, sin necesidad de que estos hayan sido etiquetados por una persona (o datos en el cual la variable de respuesta es conocida). En mis más recientes artículos, he tocado un poco de aprendizaje supervisado: por ejemplo una regresión. En estos casos, el objetivo es construir un modelo para predecir una respuesta de interés a partir de un conjunto de variables predictoras. En el caso de aprendizaje no supervisado, también se construyen modelos de los datos, pero no hay distinción entre una variable de respuesta y las variables predictoras.

Algunos ejemplos de aprendizaje no supervisado:

1. Agrupamiento o clustering
2. Reducción dimensional

En el caso de agrupamiento, se puede utilizar para identificar grupos en los datos. Por ejemplo, en una aplicación web (ej. Amazon, Netflix), se puede tener un sistema de recomendación basado en productos, o en usuarios similares (que pueden ser agrupados en base a ciertas características).

En el caso de reducción dimensional, el objetivo puede ser reducir las dimensiones de los datos a un conjunto de variables que sea más manejable. Esta reducción de variables puede ser utilizada como entrada a modelos predictivos de clasificación o regresión, por ejemplo. O por otro lado, queremos encontrar información subyacente (o latente) en los datos, que puede estar aproximada por múltiples predictores.

Como ejemplo personal, en mi proyecto open-source TRUNAJOD (Github TRUNAJOD), para explicar al usuario variables de la complejidad textual, básicamente se reduce una gran gama de predictores, en 5 predictores globales de complejidad textual, mediante una técnica llamada análisis factorial.

Dimensionalidad

Los modelos predictivos que hemos visto hasta ahora requieren como entrada un conjunto de datos, que consiste en una variable objetivo y una serie de predictores que idealmente se relacionan con esta variable. Esta serie de predictores, que usualmente son las columnas de nuestro conjunto de datos tabular, pueden ser vistos como vectores matemáticos, en donde cada dimension es un atributo (columna).

Podríamos decir, que nuestro conjunto de datos representado por una “tabla” de $M\times N$, consiste en $M$ observaciones y $N$ atributos. Esta cantodad $N$ de atributos, es lo que se conoce como dimensionalidad. Entonces, en esencia, la dimensionalidad de nuestros datos, dependerá de la cantidad de atributos que consideremos por registro.

Es intuitivo pensar que al tener mayor cantidad de atributos (es decir, mayor dimensionalidad), en teoría podríamos tener un mejor modelo, ya que estaríamos entregando mayor cantidad de información al modelo predictivo. Sin embargo, al aumentar la dimensionalidad, pueden surgir ciertos inconvenientes:

• Imaginemos que tenemos $N$ atributos binarios, es decir, tenemos observaciones de la forma $(0, 1, 1, \ldots, 1)$. Para al menos lograr ver todas las combinaciones posibles, necesitariamos $2^N$ registros. Esto es intuitivo, si nuestro modelo requiere más atributos, tendrá más variabilidad y en consecuencia requerirá mayor cantidad de registros para poder ajustar un modelo robusto.
• Los algoritmo para ajustar modelos tienen complejidades asintóticas (cómo varía cierta métrica cuando el tamaño de la entrada crece) que dependen de $M$ y $N$, por lo tanto, se volverán imprácticos de ajustar en algunos casos. En otros casos, y esto es intuitivo, el tiempo de ejecución aumentará (más información que procesar).
• Si necesito además tomar alguna decisión respecto al análisis de datos ¿Qué podría concluir de un modelo con cientos de atributos? Idealmente, debiese haber alguna forma de reducir la cantidad de dimensiones para facilitar la interpretación (ya sea eliminando atributos poco relevantes, o combinando atributos que aproximan propiedades latentes o intrínsecas similares.)
• Algo no tan intuitivo, algunos algoritmos para ajuste de modelos padecen lo que se conoce como maldición de la dimensionalidad, es decir que a medida que aumenta la dimensionalidad, el rendimiento comienza a deteriorarse (por ejemplo, aumento en la varianza del error esperado).

Existen diferentes manifestaciones de la maldición de la dimensionalidad, por lo que el lector puede investigar sobre ellas en caso de estar interesado en el tema. Supongamos que queremos implementar un algoritmo de clasificación que se base en la similitud de registros para determinar la clase a la que pertenece el registro nuevo (por ejemplo, distancia entre vectores). Supongamos que los datos consisten en puntos distribuídos en un hiper-cubo de dimensión $p$ (ejemplo: En dos dimensiones sería un cuadrado de lado 1, en 3 dimensiones un cubo de lado 1, y ya desde 4 dimensiones hacia arriba, no podemos visualizarlo jeje). Consideremos ahora una vecindad hipercúbica de puntos al rededor de un registro objetivo (punto a clasificar), que captura una fracción $r$ de las observaciones.

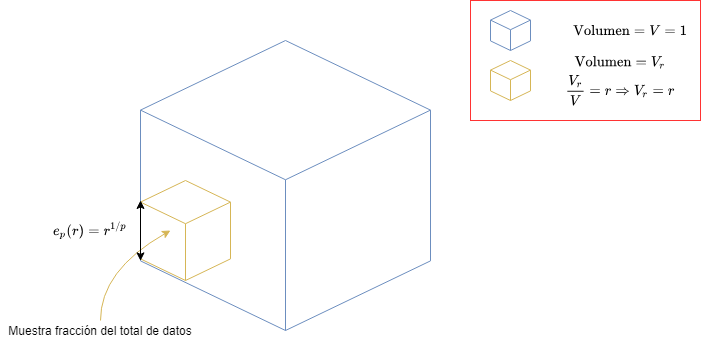
Fig 1: Ilustración de la maldición de la dimensionalidad.

Si quisieramos calcular el largo de los lados del hipercubo que contiene una fración $r$ del volumen del total de datos, entonces el largo sería $e_p(r) = r^{1/p}$. Consideremos una dimensionalidad de 10 atributos ($p = 10$), entonces $e_{10}(0.01) = 0.63$ y $e_{10}(0.1) = 0.80$, cuando el rango total de cada entrada (valor de cada atributo) es sólo 1 (hipercubo unitario). Esto quiere decir, que para calcular el $1\%$ o el $10\%$ de los datos para conformar un promedio local, debemos cubrir el $63\%$ o el $80\%$ del rango de cada variable de entrada. Por lo tanto, dichas vecindades, que en dimensionalidades pequeñas eran locales, dejan de ser locales en dimensionalidades altas. Reducir $r$ no ayudaría, pues tendríamos menos observaciones que promediar y por lo tanto la varianza de nuestro ajuste aumentaría.

Por otro lado, se puede demostrar cómo las métricas de distancia se ven afectadas dependiendo de la cantidad de muestras y de la dimensionalidad. Sin embargo, para no complicar la matemática, sólo obtendremos la intuición de forma experimental. En el siguiente experimento, podemos observar qué pasaría con las métricas de distancia, a medida que aumenta dimensionalidad:

import matplotlib.pyplot as plt
import numpy as np
import pandas as pd

from scipy.spatial.distance import cdist


%matplotlib inline

plt.style.use("seaborn")
plt.rcParams["figure.figsize"] = (6, 3)
plt.rcParams["figure.dpi"] = 200


def get_avg_max_min_dist_ratio(dataset):
    """Retorna proporcion entre maxima y minima distancia euclideana de un dataset.

    :param dataset: Conjunto de datos.
    :type dataset: pd.numpy.array
    :return: Promedio proporción de maxima/minima distancia de cada punto
    :rtype: float
    """
    euclidean_dist = cdist(dataset, dataset)

    # Encontrar minimos que no sean 0
    min_dist = np.zeros(len(dataset))
    for i, row in enumerate(euclidean_dist):
        min_dist[i] = np.amin(row[row != 0])
    max_dist = np.amax(euclidean_dist, 1)
    return np.mean(max_dist/min_dist)

# Tamaño de conjunto de datos
M = 1000
dimensionalities = (2, 5, 10, 20, 30, 50, 70, 80, 100)
avg_farthest_distances = np.zeros(len(dimensionalities))

for k, N in enumerate(dimensionalities):
    dataset = np.random.normal(0, 10, size=(M, N))

    # Calcular distancia promedio maxima de puntos respecto a cualquier otro punto
    avg_farthest_distances[k] = get_avg_max_min_dist_ratio(dataset)

plt.plot(dimensionalities, avg_farthest_distances, "o")
plt.xlabel("Dimensionalidad")
plt.ylabel(r"$Promedio\left(\frac\right)$")
plt.title("Media de proporción entre distancia máxima y mínima \nvs Dimensionalidad")

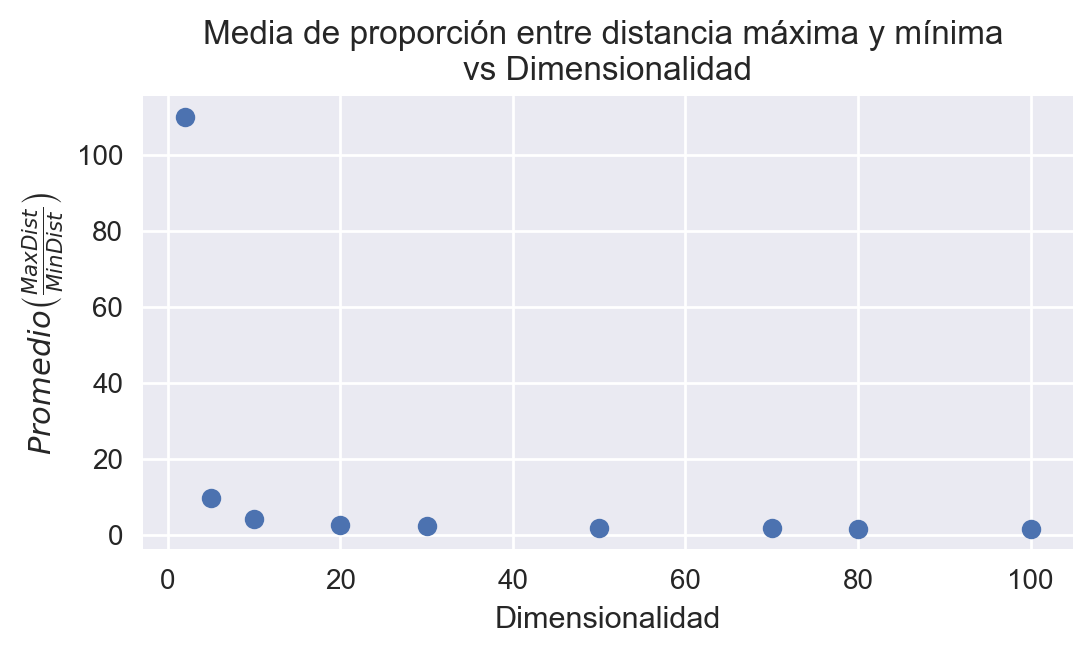
Fig 2: Proporción de máxima distancia-mínima distancia respecto a la cantidad de dimensiones.

print(f"Dimensionalidad 5: {get_avg_max_min_dist_ratio(np.random.normal(0, 10, size=(M, 5)))}")
print(f"Dimensionalidad 500: {get_avg_max_min_dist_ratio(np.random.normal(0, 10, size=(M, 500)))}")

Dimensionalidad 5: 9.33633957667241
Dimensionalidad 500: 1.1948297526920728

Podemos observar por ejemplo, que en promedio, la proporción entre la máxima y mínima distancia entre los puntos es 9.34 para N = 5 y 1.19 para N = 500. Esto quiere decir que en el primer caso, el la distancia máxima puede llegar a ser hasta 10 veces mayor que la distancia mínima para una dimensionalidad pequeña, pero sólo de un 19% para una dimensionalidad de 500. Esto quiere decir, que en esencia, la información que nos entrega la distancia entre los puntos es casi nula, lo que podría afectar la varianza en las predicciones aunque el sesgo sea bajo; y por lo tanto, afectar el rendimiento del modelo predictivo.

Reducción de Dimensionalidad

Como hemos visto hasta ahora, tener alta dimensionalidad puede causar algunos problemas:

• Difícil visualización de datos e interpretación (ej. tener demasiadas variables predictoras)
• Maldición de la dimensionalidad, la distancia entre puntos de un espacio tiende a ser insignificante en altas dimensiones.
• Variabilidad y dispersión de datos. Por ejemplo cuando se trabaja con textos y consideramos la frecuencia de diferentes términos como datos, se trabaja con altas dimensionalidades que además, por la naturaleza del problema, tienden a generarse matrices dispersas. En estos casos la reducción dimensional permite reducir la variabilidad en los datos.
• En algunos casos, es costoso computacionalmente en términos de rendimiento y uso de memoria, considerar una elevada cantidad de atributos. Por lo que, la reducción dimensional permite reducir estos problemas.

Existen diferentes métodos de reducción dimensional, pero en este curso veremos en particular dos: Análisis de Componentes Principales, del inglés PCA Principal Component Analysis, y Análisis Factorial (Factor Analysis). Estos métodos tienen algunos supuestos, que en algunos casos los hacen poco útiles. Por ejemplo para visualización de datos, existen también otros métodos como: Multidimensional Scaling (MDS), T-SNE, Non-Linear PCA, entre otros.

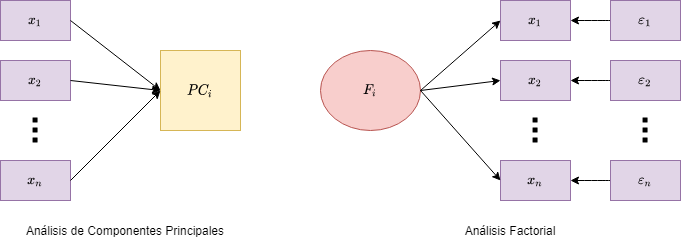
Fig 3: Análisis factorial vs PCA.

El enfoque de PCA para reducción dimensional es básicamente crear una o más variables a partir de un conjunto de variables medidas. Lo que hace es en esencia crear una combinación lineal de estas nuevas variables, que idealmente reproducen las variables medidas. El enfoque en el análisis factorial (utilizado comúnmente en psicometría) es modelar una variable latente/subyacente a partir de un conjunto de mediciones. En simples términos, los factores a obtener están causando las respuestas en las variables medidas (y sus relaciones), es por ello, que en la figura 3 se muestra la flecha en sentido contrario al caso de PCA. El modelo factorial también considera un término de error, que en esencia toma la variabilidad que no puede ser explicada únicamente por el factor. En las siguientes secciones se revisarán en mayor detalle estos métodos.

Análisis Factorial

Los datos multi-variados usualmente son vistos como mediciones indirectas de propiedades subyacentes que no pueden ser medidas directamente. Algunos ejemplos:

• Pruebas educacionales y psicológicas utilizan cuestionarios, y usan las respuestas a estos cuestionarios para medir variables subyacentes como la inteligencia u otras habilidades mentales de los sujetos.
• Los electroencefalogramas se utilizan para medir actividad neuronal en varias partes del cerebro, mediante mediciones de señales electromagnéticas registradas por sensores ubicados en distintas posiciones de la cabeza del sujeto.
• Los precios del mercado de acciones cambian constantemente a lo largo del tiempo, y reflejan varios factores que no están medidos, tales como confianza en el mercado, influencias externas, y otras fuerzas que pueden ser difíciles de identificar o medir.
• En caso particular del projecto TRUNAJOD, se intenta medir la complejidad del texto a partir de ciertas propiedades extrínsicas de los mismos. ¿Se puede medir complejidad textual directamente?

El análisis factorial es una técnica estadística clásica cuyo objetivo es identificar esta información latente (subyacente). Los análisis factoriales están típicamente ligados a distribuciones Gaussianas, lo que reduce su utilidad en algunos casos.

En esencia los factores están asociados con múltiples variables observadas, que tienen ciertos patrones similares. Cada factor explica una cantidad particular de la varianza en los datos observados. Esto ayuda en la interpretación de los datos, reduciendo la cantidad de variables:

$$X_i = \beta_{i0} + \beta_{i1} F_1 + \ldots \beta_{il}F_l + \varepsilon_i$$

Esto lo podemos visualizar como se muestra en la figura 4.

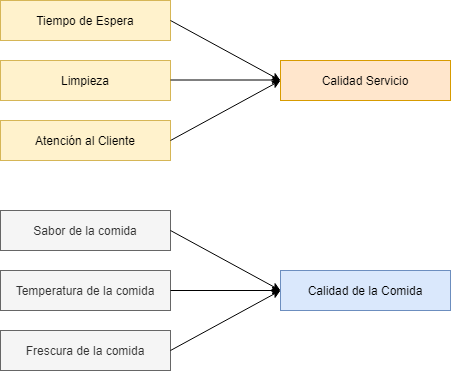
Fig 4: Ejemplo de factores.

Cabe destacar que existen dos tipos de análisis factoriales: Análisis Factorial Exploratorio y Análisis Factorial Confirmatorio. El primero, se enfoca en explorar posibles relaciones, mientras que el segundo se enfoca en confirmarlas (teniendo obviamente una hipótesis de la relación de las variables).

Por otro lado, al hacer un análisis factorial, se deben tener las siguientes consideraciones:

• No hay outliers en los datos.
• El tamaño de la muestra es mayor que la cantidad de factores a considerar.
• No debe haber multi-colinealidad (una columna sea combinación lineal de otra).
• No existe homocedasticidad entre las variables.

Analizaremos los datos de la encuesta del Centro de Estudios Públicos realizada en Junio del 2003. Parte del conjunto de preguntas está asociado a preguntas sobre el nivel de confianza institucional. Para más información pueden revisar este enlace: Estudio Nacional de Opinión Pública N°45, Junio-Julio 2003.

import factor_analyzer as factor
import missingno as msngo
import pandas as pd


df = pd.read_csv("datos/cep45.csv")
df.head()

Extraeremos los datos de las preguntas (valores 8 y 9 significa que no hay información, ver detalle en el enlace mencionado):

trust_df = df.filter(regex="p17_*")
trust_df = trust_df.rename(
    columns={
        "p17_a": "I.Catolica",
        "p17_b": "I.Evangelica",
        "p17_c": "FFAA",
        "p17_d": "Justicia",
        "p17_e": "Prensa",
        "p17_f": "Television",
        "p17_g":"Sindicatos",
        "p17_h":"Carabineros",
        "p17_i": "Gobierno",
        "p17_j": "PartidosPol",
        "p17_k": "Congreso",
        "p17_l":"Empresas",
        "p17_m":"Universidades",
        "p17_n":"Radio"
})

Podemos explorar la base de datos para visualizar los registros incompletos:

import matplotlib.pyplot as plt
import numpy as np

%matplotlib inline

plt.style.use("seaborn")
plt.rcParams["figure.figsize"] = (6, 4)
plt.rcParams["figure.dpi"] = 200

plt.figure(figsize=(4,4))
msngo.matrix(trust_df.replace([8, 9], [np.nan, np.nan]))

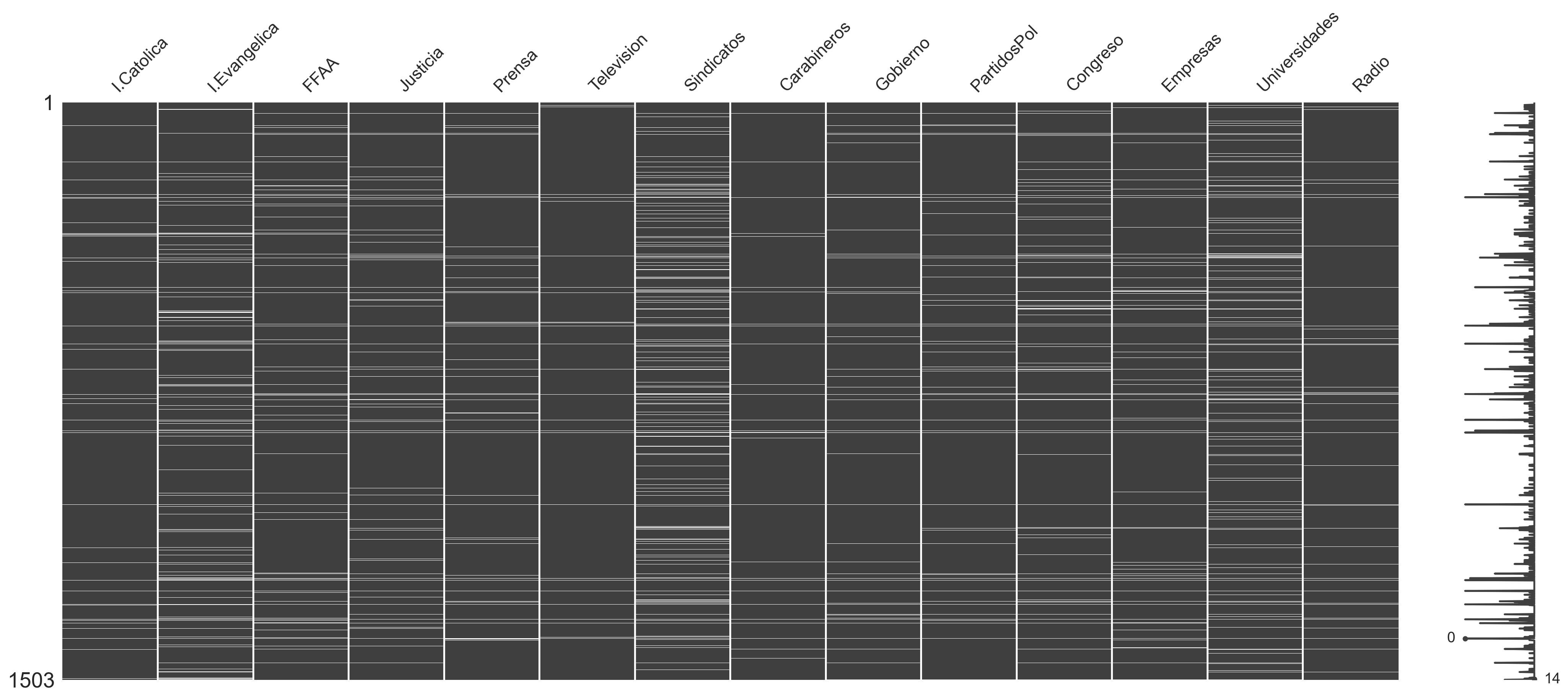
Fig 5: Visualización de datos incompletos.

Ahora analicemos las medias para cada pregunta:

trust_df.replace([8, 9], [np.nan, np.nan], inplace=True)
trust_df.dropna(inplace=True)
means = trust_df.mean().sort_values()
plt.plot(means.values, means.index, "bo")

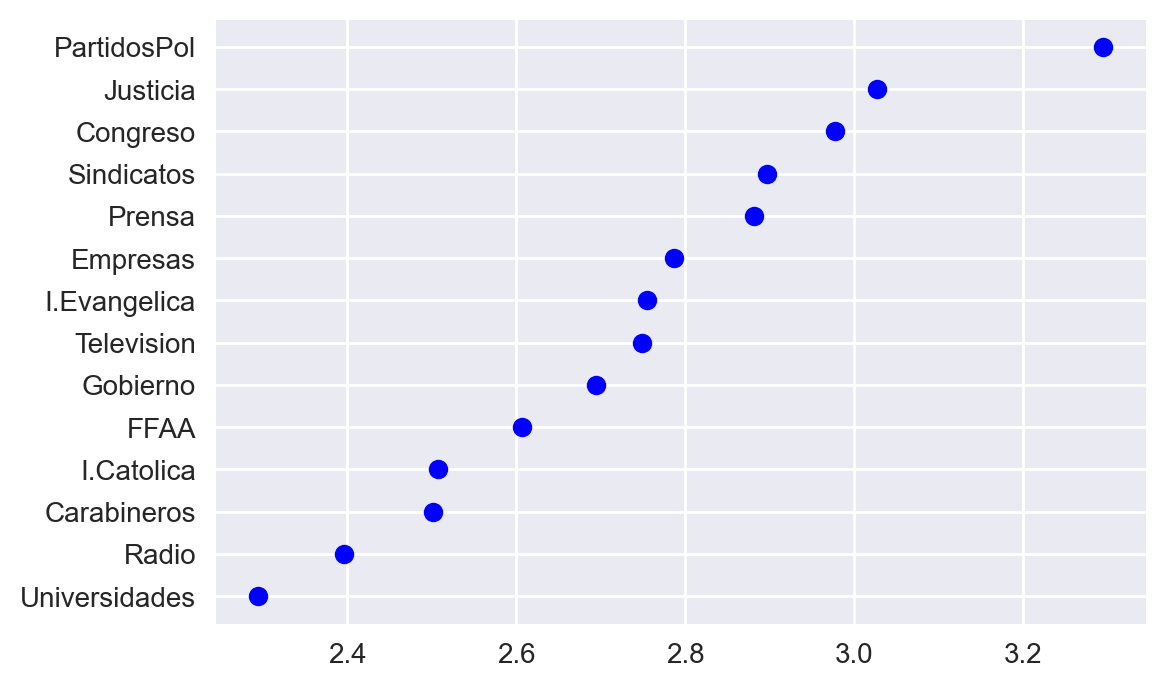
Fig 6: Media de los atributos del ejemplo.

Mientras mayor sea el valor, significa que los encuestados confían menos en dicha entidad. Se puede observar por ejemplo que los encuestados confían menos en Partidos Políticos, Sindicatos, Justicia y Congreso.

Ahora vamos a proceder a hacer un análisis factorial. Sin embargo, antes de realizar este análisis, se debe hacer una prueba de adecuación, que básicamente responde a la pregunta ¿Podemos encontrar factores en nuestro conjunto de datos? Existen dos métodos (quizás más) para verificar la adecuación de la muestra de datos para un análisis factorial:

• Prueba de Bartlett
• Prueba de Kaiser-Meyer-Olkin (desde ahora KMO)

La prueba de Bartlett es una prueba de hipótesis que verifica si existe correlación entre las variables, y lo que hace es comparar la matriz de correlación de la muestra con una matriz identidad (es decir, que no haya correlación). Si la diferencia no es significativa, entonces no deberíamos aplicar análisis factorial.

import factor_analyzer as fact


chisq, pvalue = fact.calculate_bartlett_sphericity(trust_df)
print(f"Chi-Cuadrado: {chisq}, p-value: {pvalue}")

Chi-Cuadrado: 2897.0676232781584, p-value: 0.0

En este caso, el p-value es 0, por lo que podemos rechazar la hipótesis de que no hay correlación en los datos.

La prueba de Kaiser-Meyer-Olkin (KMO) miden la idoneidad de los datos para un análisis factorial. Determina la adecuación para cada variable observada y para el modelo completo. La prueba de KMO estima la proporción de varianza entre todas las variables observadas. Los valores de KMO están entre 0 y 1. Un valor de KMO menor que 0.6 se considera inadecuado:

kmo_all, kmo_model = fact.calculate_kmo(trust_df)
print(f"Valor KMO para el modelo: {kmo_model}")

Valor KMO para el modelo: 0.8299274694302806

En este caso obtenemos un valor de 0.83, lo que cumple el requisito para que el análisis factorial sea adecuado. Ahora procederemos a realizar el análisis factorial. Para escoger la cantidad de componentes, por lo general se hace un scree plot que básicamente grafica cada uno de los valores propios (básicamente la varianza explicada por cada factor de la varianza total), y se escogen los valores propios que sean mayores que 1:

factorize = fact.FactorAnalyzer(rotation="varimax")
factorize.fit(trust_df)
factor_screeplot = factorize.get_eigenvalues()[0]

plt.plot(range(1, len(factor_screeplot) + 1), factor_screeplot, "o-", color="tomato")
plt.xlabel("Número de Factor")
plt.ylabel("Valores Propios")
plt.axhline(1)
plt.title("Scree plot")

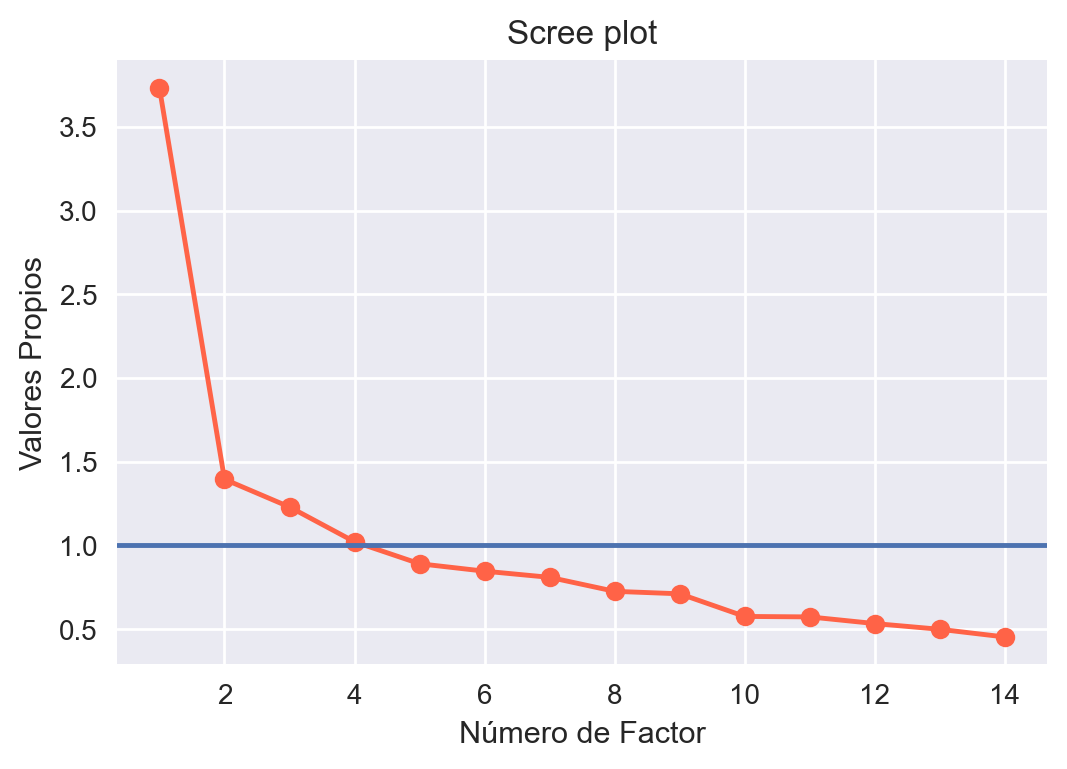
Fig 7: Valores propios vs número de factores.

De los resultados, podemos observar que podemos escoger 4 factores. Luego podemos ver las cargas de cada factor. Las cargas factoriales son básicamente las relaciones de cada factor con cada variable:

factorize = fact.FactorAnalyzer(n_factors=4, rotation="varimax")
factorize.fit(trust_df)
factor_loadings = pd.DataFrame(
    factorize.loadings_,
    index=trust_df.columns,
    columns=("Factor 1", "Factor 2", "Factor 3", "Factor 4"))
factor_loadings

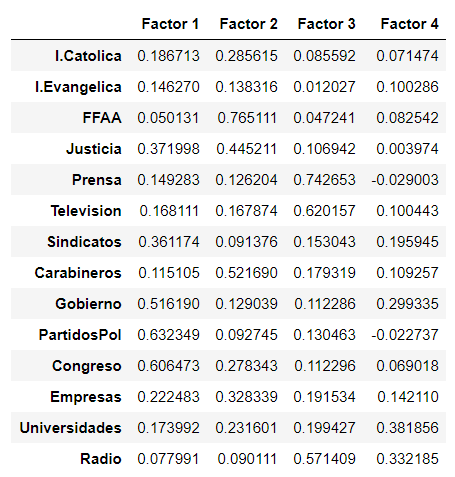
La matriz anterior es un poco complicada de interpretar. Por lo general, un criterio de corte para las cargas factoriales, es remover los factores cuya carga factorial sea menor que 0.4, haremos eso procesando los datos:

factor_loadings.where(factor_loadings >= 0.4, "")

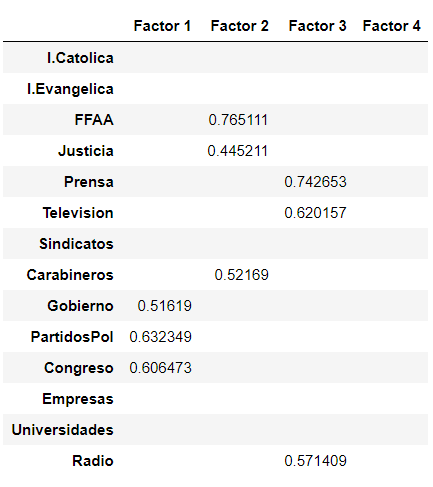
Observamos que el factor 4 fue descartado, debido a que el criterio de corte, consideró que las cargas factoriales no estaban por sobre el umbral. En el resto de los factores, podemos hacer la siguiente interpretación: El factor 1, corresponde a medidas relacionadas a como los encuestados ven al gobierno, y temas relacionados a la política. El factor 2 está relacionado con componentes de justicia, como las fuerzas armadas, justicia y carabineros. El factor 3 está relacionado a la confianza de la gente en los medios de prensa. Y las variables como iglesia Católica, iglesia evangélica, sindicatos, empresas y universidades, no presentan carga significativa en ninguno de los factores. Probablemente por alta cantidad de datos incompletos, entre otras cosas.

Finalmente observamos que los tres factores escogidos explican aproximadamente un 31% de la varianza en los datos:

pd.DataFrame(
    np.vstack(factorize.get_factor_variance()),
    index=("SS Loadings", "Proportion Var", "Cumulative Var"),
    columns=("Factor 1", "Factor 2", "Factor 3", "Factor 4"))

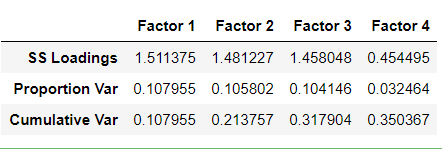
Observamos que el cuarto factor tiene un SS loadings bajo. El SS loading es la suma cuadrática de las cargas factoriales. Generalmente se conservan los factores cuya suma cuadrática de cargas sea mayor que 1 (consistente con el criterio de corte, ya que vemos que el factor 4, tiene un valor menor que uno).

Finalmente, por completitud, si quieren transformar las observaciones a factores, tienen que usar el método transform como sigue:

# Nos dimos cuenta que solo son 3 factores los relevantes
factorize = fact.FactorAnalyzer(n_factors=3, rotation="varimax")
factorize.fit(trust_df)
transformed_df = pd.DataFrame(
    factorize.transform(trust_df),
    columns=("Factor 1", "Factor 2", "Factor 3", "Factor 4"))
transformed_df.head()

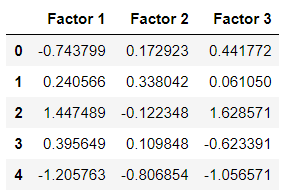
Análisis de Componentes Principales

Primero, es interesante entender qué significa componentes principales, y cuál es la intuición. En términos simples, las componentes principales serían ejes en donde ocurre la máxima variación en los datos. En términos simples, podrían verse las componentes principales como un cambio de sistema de coordenadas, o un cambio de vectores bases. Por ejemplo, una transformación de un sistema de coordenadas a otro, podría ser como sigue:

$$ x_1 \begin{bmatrix} a \\\ c \end{bmatrix} + x_2 \begin{bmatrix} b \\\ d \end{bmatrix} = \begin{bmatrix} ax_1 + bx_2 \\\ cx_1 + dx_2 \end{bmatrix} $$

En este caso, los vectores en el lado izquierdo son vectores base, como referencia:

• $[a, c]$ ; $[b, d]$ son los vectores base
• En el sistema cartesiano convencional, los vectores base son $[1, 0]$; $[0, 1]$ (o comunmente $x$ e $y$)

No cualquier vector puede ser un vector base, algunos puntos clave:

• Los vectores base son los mismos para todos los registros de un conjunto de datos.
• Los vectores base son ortonormales, es decir, perpendiculares entre sí y con norma 1 (largo 1)
• Finalmente, podemos representar cada registro del conjunto de datos como una combinación lineal de sus vectores base.

Lo anterior puede verse abstracto, por lo que tomemos un ejemplo:

def draw_vector(v0, v1, ax=None):
    ax = ax or plt.gca()
    arrowprops=dict(
        arrowstyle="->",
        linewidth=2,
        shrinkA=0, shrinkB=0,
        color="b")
    ax.annotate("", v1, v0, arrowprops=arrowprops)

rng = np.random.RandomState(1)
X = np.dot(rng.rand(2, 2), rng.randn(2, 200)).T
plt.scatter(X[:, 0], X[:, 1])


pca = pca = PCA(n_components=2)
pca.fit(X)
X_pca = pca.transform(X)


plt.plot(X[:, 0], X[:, 1], "ro")
for length, vector in zip(pca.explained_variance_, pca.components_):
    v = vector * 3 * np.sqrt(length)
    draw_vector(pca.mean_, pca.mean_ + v)

plt.title("Ilustración PCA")
plt.xlabel("$x_1$")
plt.ylabel("$x_2$")
plt.axis("equal")

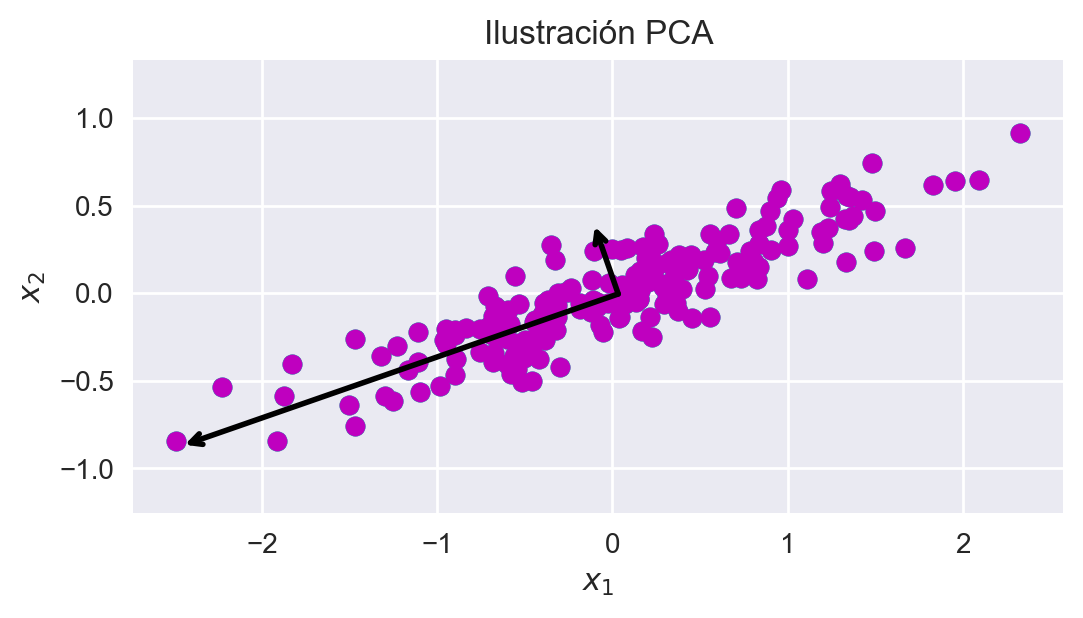
Fig 8: Ilustración de PCA.

Como se observa en la figura, el conjunto de datos llevarse a otro sistema de coordenadas considerando estos vectores base (para transformar los datos, basta simplemente con aplicar la transformación lineal descrita). Podemos ver también que cada eje se escoge en la dirección donde haya mayor variabilidad en los datos (varianza).

Un ejemplo de aplicación de las componentes principales, es en el caso de reducción dimensional. Por ejemplo, podemos eliminar las componentes con menor cantidad de varianza, es decir, que explican menos la variabilidad en los datos, y en consecuencia, estaríamos proyectando el espacio dimensional en un espacio de menos dimensiones. Para ilustrar esto, consideremos el siguiente ejemplo:

from mpl_toolkits.mplot3d import Axes3D


plt.rcParams["figure.figsize"] = (10, 10)

EJEMPLO_PCA_URL = (
    "https://gist.githubusercontent.com/dpalmasan/"
    "1bba35979f1f284ddf7c8c540f60c66f/raw/"
    "4a3fcf2f97fa2d85be69eedaa98b0ed6f46a3017/tetra.csv"
)
df = pd.read_csv(EJEMPLO_PCA_URL)

pca = pca = PCA(n_components=2)
pca.fit(df)
X_pca = pca.transform(df)

fig = plt.figure()
ax = fig.add_subplot(211, projection="3d")
ax.scatter(df["x"], df["y"], df["z"], c="b", marker="o")
ax.set_xlabel("X")
ax.set_ylabel("Y")
ax.set_zlabel("Z")
ax.set_title("Tetera en 3D")
ax = fig.add_subplot(212)
ax.plot(X_pca[:, 0], X_pca[:, 1], "ro")
ax.set_xlabel("PC 1")
ax.set_ylabel("PC 2")
ax.set_title("Proyección en 2D de la tetera (sombra)")

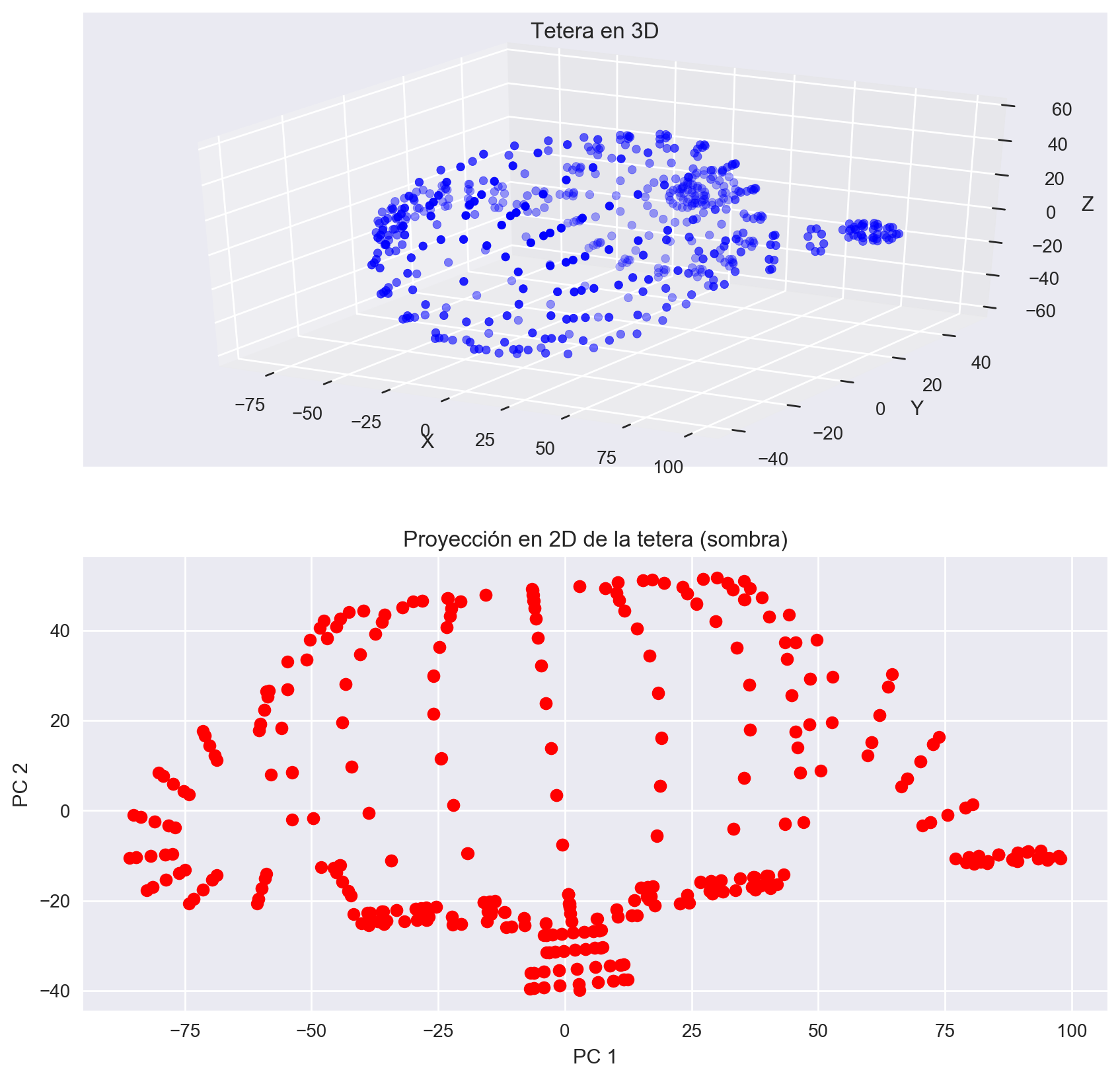
Fig 9: Intuición PCA.

En el ejemplo de la tetera, básicamente tenemos un espacio dimensional de 3 dimensiones (x, y, z). Cuando aplicamos PCA y eliminamos una componente (la de menos variación), básicamente estamos calculando una proyección de este espacio a un espacio de menor dimensión, intentando mantener la variabilidad del espacio original. Intuitivamente, en este caso particular, podría pensarse en cada componente principal como visualizar la “sombra” de la tetera. Claro, que no estamos restringidos sólo a espacios de 3 dimensiones, si no que también podemos reducir espacios de cualquier dimension a uno de menor dimensionalidad, por ejemplo, para visualizar datos.

Consideremos los datos de World Wealth and Income Database.

from sklearn.decomposition import PCA
from sklearn.preprocessing import StandardScaler


df = pd.read_csv("income-db.csv")
scaler = StandardScaler()

X = df.select_dtypes(exclude=["object"])
X = scaler.fit_transform(X)
pca = pca = PCA(n_components=2)
pca.fit(X)

# Transformar a dos dimensiones
X = pca.transform(X)

income_greater = df["income"] == ">50K"
income_leq = df["income"] == "<=50K"
plt.plot(X[income_greater, 0], X[income_greater, 1], "ro", alpha=0.7)
plt.plot(X[income_leq, 0], X[income_leq, 1], "bo", alpha=0.7)
plt.legend(("income > 50K", "income <= 50K"))
plt.xlabel("componente principal 1")
plt.ylabel("Componente principal 2")
plt.title("Proyección datos numéricos con PCA")

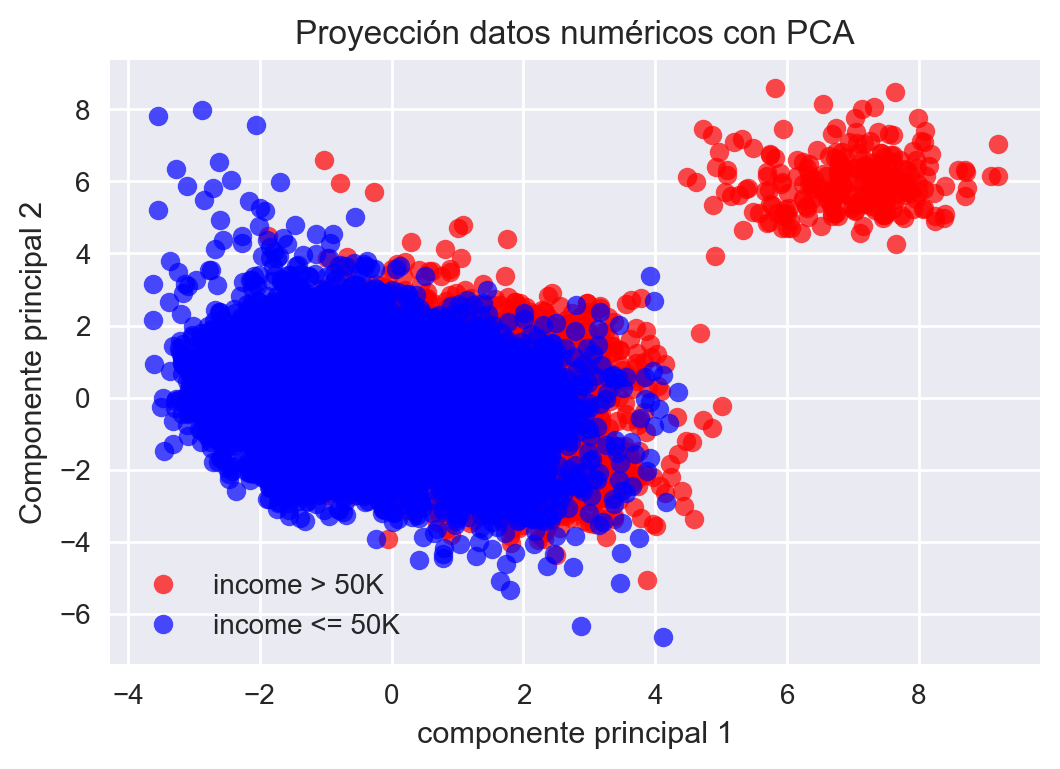
Fig 10: Ejemplo PCA.

Además, podemos ver cómo impacta cada variable a cada nueva dimensión:

# El signo no importa, importa el signo relativo, podemos ver
# Cómo afecta cada componente a cada variable por ejemplo
pd.DataFrame(
    pca.components_,
    columns=df.select_dtypes(exclude=["object"]).columns,
    index = ["PC-1", "PC-2"])

Debe considerarse también, que usualmente se estandarizan los datos antes de aplicar PCA (por ejemplo normalizar, o llevar a una misma escala), por lo tanto, cuando lo apliquen, hagan este pre-procesamiento antes. Finalmente, y recapitulando hasta ahora, PCA es un maximizador de varianza, que proyecta los datos originales en las direcciones donde la varianza es máxima.

Ejemplo Datos MNIST (dígitos manuscritos)

Finalmente, por completitud, haremos el ejemplo típico de analizar el conjunto de datos de reconocimiento de dígitos, que en esencia consiste en imágenes de 8x8 donde cada imagen contiene un dígito manuscrito.

from sklearn.datasets import load_digits


digits = load_digits()
print(digits.keys())
print(digits.data[0])
print(digits.target[0])
print(digits.feature_names)

Por ejemplo, miremos un dígito arbitrario:

import matplotlib.pyplot as plt


%matplotlib inline

plt.style.use("seaborn")
plt.rcParams["figure.figsize"] = (6, 4)
plt.rcParams["figure.dpi"] = 200

plt.imshow(digits.data[1].reshape((8, 8)))
plt.title((f"Imagen de {digits.target[1]}"))

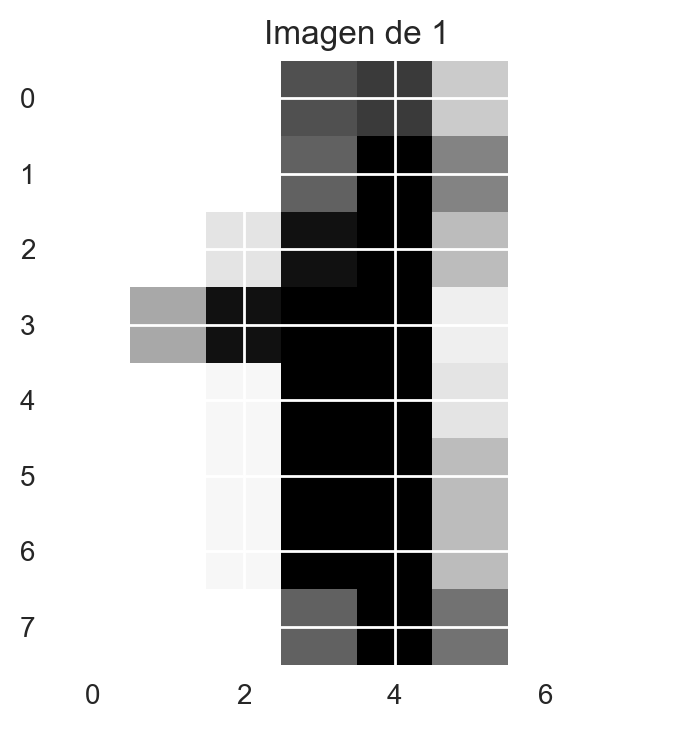
Fig 11: Muestra conjunto de datos de dígitos.

Como los datos son de imágenes de 8x8 píxeles, básicamente cada atributo es el valor del píxel (en escala de grises), por lo tanto se tienen 64 atríbutos por registros. Dada la naturaleza del problema, PCA pareciera ser una buena opción para visualizar atributos similares en los dígitos (por ejemplo curvatura, simetría, etc.):

from sklearn.decomposition import PCA


# Contrario a lo que dice la lectura, PCA NO llama a StandardScaler por debajo
# Lo que sí hace es centrar los datos pero NO los escala
# En este caso da igual, porque todos los atributos están en la misma escala
pca = PCA(n_components=2)
X_pca = pca.fit_transform(digits.data)
print(f"Dimensionalidad original: {digits.data.shape}")
print(f"Dimensionalidad después de PCA: {X_pca.shape}")

En este caso, transformaremos a dos componentes, para hacer una visualización en 2D y dar un vistazo a si existe alguna relación en los registros:

plt.scatter(X_pca[:, 0], X_pca[:, 1],
    edgecolor="none",
    c=digits.target,
    alpha=0.7,
    cmap="Set1")
plt.colorbar()
plt.xlabel("PC 1")
plt.ylabel("PC 2")
plt.title("Dígitos proyectados a dos dimensiones")

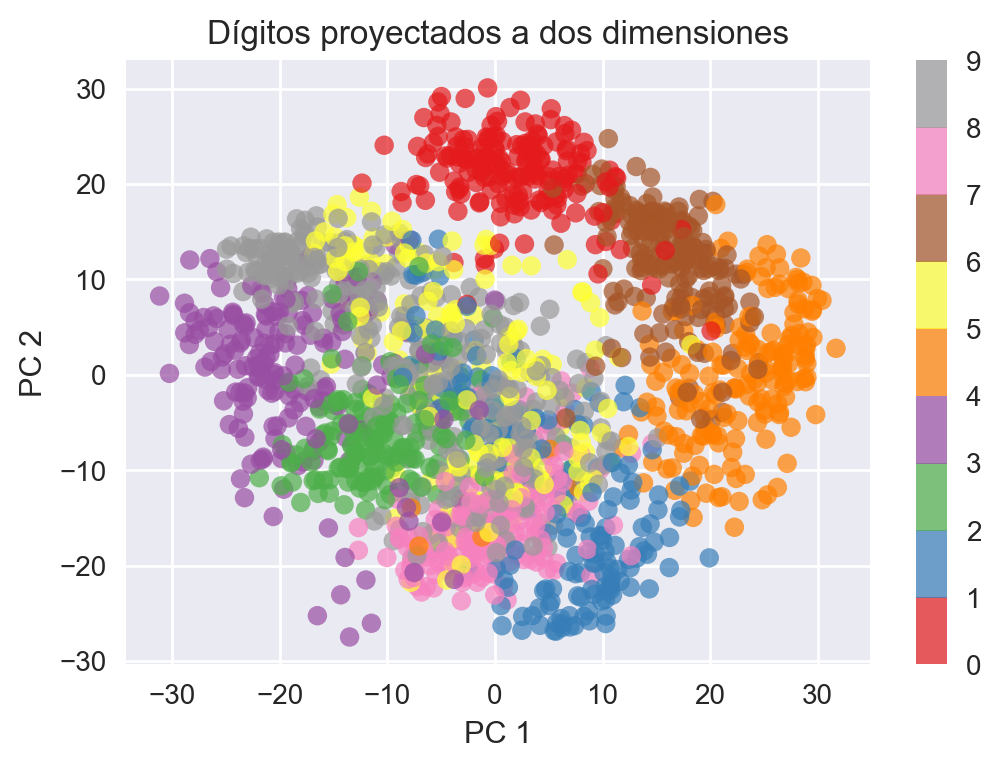
Fig 12: Imágenes de dígitos manuscritos proyectados en un espacio bi-dimensional.

De la figura se pueden desprender algunas relaciones interesantes. Por ejemplo, el 4 está cerca del 9, probablemente porque tienen formas similares, lo mismo el 3 con el 8. También vemos que en general los dígitos están agrupados en distintas porciones del espacio.

Para elegir la cantidad de componentes, en general se debe tener un umbral de cuánta información de los datos se quiere retener, o en términos matemáticos, cuánta varianza explicada en los datos se quiere considerar. Para ello podemos hacer el siguiente gráfico:

pca_full = PCA().fit(digits.data)
plt.bar(range(1, pca_full.n_components_ + 1), pca_full.explained_variance_ratio_,
        label="Varianza por componente")
plt.step(range(1,len(pca_full.components_) + 1), np.cumsum(pca_full.explained_variance_ratio_),
color="tomato", label="Varianza acumulada")
plt.xlabel("Cantidad de Dimensiones")
plt.ylabel("Varianza")
plt.legend()

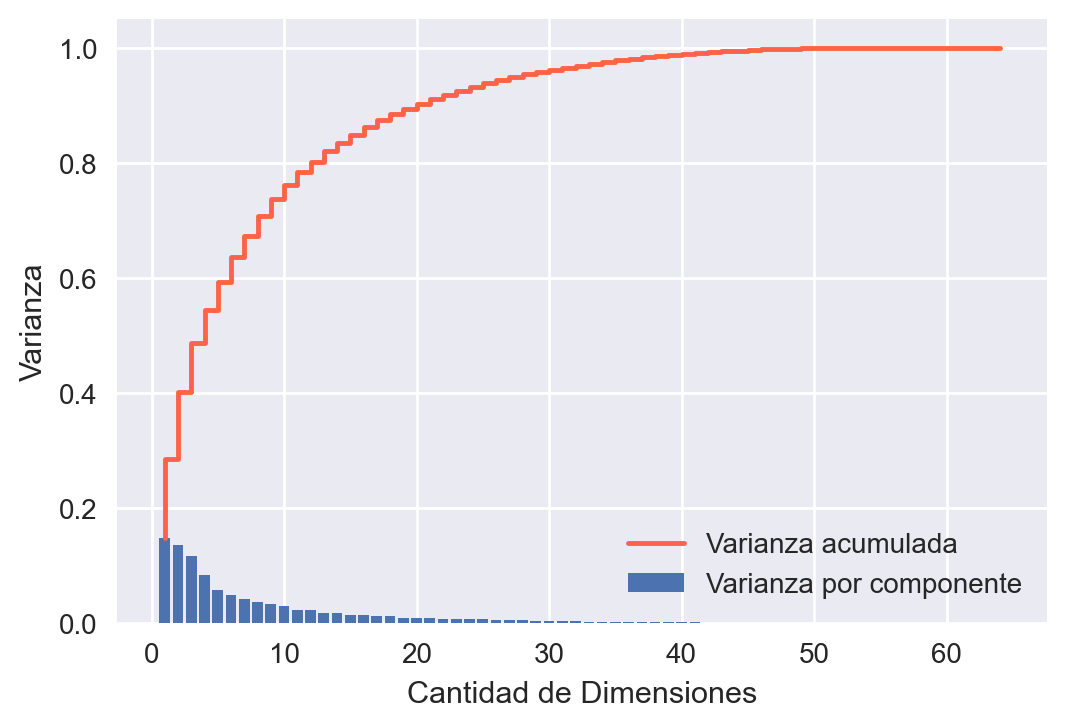
Fig 13: Varianza acumulada respecto a la cantidad de dimensiones.

En este caso, podemos ver que alrededor de 10 componentes debería ser suficiente para explicar gran cantidad de la varianza en los datos (entre 0.7 y 0.8). Esto también se puede usar como “filtro”, ya que quizás, mayores componentes estén ajustandose al ruido en los datos. Finalmente, visualicemos cómo contribuye cada componente a cada dígito:

def show(fig, grid, i, j, x, imshape, fontsize, title=None):
    """
    Función auxiliar para agregar gráficos a la figura.
    """
    ax = fig.add_subplot(grid[i, j], xticks=[], yticks=[])
    ax.imshow(x.reshape(imshape), interpolation="nearest", cmap="Blues")
    if title:
        ax.set_title(title, fontsize=fontsize)



def plot_pca_components(x, coefs=None, mean=0, cmps=None,
                        imshape=(8, 8), n_components=10, fontsize=12,
                        show_mean=True):
    """
    Graficar componentes PCA para dataset de dígitos.
    """
    if coefs is None:
        coefs = x

    if cmps is None:
        cmps = np.eye(len(coefs), len(x))

    # Como datos fueron centrados en 0, para reconstruirlos en el espacio
    # Original, a cada componente se le agrega el promedio
    mean = np.zeros_like(x) + mean

    # Ajustar ancho y alto de figura
    fig = plt.figure(figsize=(1.2 * (5 + n_components), 1.2 * 2))

    # Crear distribución de figuras dentro del gráfico
    grid = plt.GridSpec(2, 4 + int(show_mean) + n_components, hspace=0.3)

    # Se grafica en las dos primeras filas y dos primeras columnas del plot
    show(fig, grid, slice(2), slice(2), x, imshape, fontsize, "Original")
    approx = mean
    counter = 2
    if show_mean:
        show(fig, grid, 0, 2, np.zeros_like(x) + mean, imshape, fontsize, r"$\mu$")
        show(fig, grid, 1, 2, approx, imshape, fontsize, r"$1 \cdot \mu$")
        counter += 1

    for i in range(n_components):
        # Reconstruir imagen considerando i + 1 componentes componentes
        approx = approx + coefs[i] * cmps[i]
        show(fig, grid, 0, i + counter, cmps[i], imshape,
            fontsize, r"$c_{0}$".format(i + 1))
        show(fig, grid, 1, i + counter, approx, imshape,
            fontsize, r"$ {0:.2f} \cdot c_{1}$".format(coefs[i], i + 1))
        if show_mean or i > 0:
            plt.gca().text(0, 1.05, "$+$", ha="right", va="bottom",
                          transform=plt.gca().transAxes, fontsize=fontsize)

    show(fig, grid, slice(2), slice(-2, None), approx, imshape, fontsize, "Aproximación")


pca_10 = PCA(n_components=10).fit(digits.data)
X_pca10 = pca_10.fit_transform(digits.data)
plot_pca_components(digits.data[6], X_pca10[6], pca_10.mean_, pca_10.components_)

Fig 14: Ejemplo de diferentes componentes para un dígito.

Agrupación

Existen diversos escenarios en los cuales nos gustaría agrupar los datos o encontrar grupos de datos, pues ello nos permitiría encontrar información relevante acerca de la población de datos de interés. Algunos ejemplos:

• Segmentación de clientes.
• Sistemas de recomendación.
• Categorización de diversos grupos.
• Segmentación de Imágenes.
• Entre otros.

Existen diversos métodos para agrupar datos, nosotros veremos uno bastante simple, que aún a pesar de su simpleza, se utiliza en la prácticas. El algorimo que veremos es conocido como K-means.

Clústering K-Means

La técnica de clústering consiste en dividir los datos en diferentes grupos, donde los registros en cada grupo son similares entre sí. Un objetivo del clústering es encontrar grupos interesantes de datos. Estos grupos pueden ser utilizados directamente, analizados en profunidad, o ser usados como atributos en un algoritmo de clasificación o de regresión.

El algoritmo K-means divide los datos en K clústers mediante la minimización de la suma de las distancias cuadráticas de cada registro al centro de su clúster asignado. En general la serie de pasos a seguir es la siguiente:

1. Comenzar con K centros aleatorios.
2. Asignar cada registro a un clúster en base a su distancia hacia el centro. Se asigna al clúster cuya distancia sea la mínima respecto al centro.
3. Luego, calcular el “centro de masa” de cada clúster (recalcular centros)
4. Volver al paso 2, y repetir hasta satisfacer un criterio de detención (por ejemplo que asignación no cambie entre iteraciones).

def kmeans_clustering(X, clusters=5, maxit=100):
    """Calcula clústers usando K-means.

    Este código lo hice cuando era estudiante así que está feo, me
    disculpo por eso.

    :param X: Conjunto de datos
    :type X: np.array
    :param K: Cantidad de clústers, defaults to 5
    :type K: int, optional
    :param maxit: Cantidad máxima de iteraciones, defaults to 10
    :type maxit: int, optional
    :return: (cluster_assign, centroides, iteraciones)
    :rtype: tuple(np.array, np.array, int)
    """
    # Sample Size
    N = X.shape[0]

    # Inicializar vector de clústers
    c = np.zeros(N)

    # Inicializar centroides, se escogen al azar datos del conjunto de datos
    mu = X[np.random.choice(N, clusters, replace=False), :]

    # Asignar datos a cada clúster
    for i in range(N):
        kmin = 1
        min_dist = float("Inf")
        for k in range(clusters):
            dist = np.linalg.norm(X[i, :] - mu[k, :])
            if dist < min_dist:
                min_dist = dist
                kmin = k
        c[i] = kmin + 1


    c_new = np.zeros(N)
    it = 1

    # Iterar hasta máximo de iteraciones o hasta que no haya cambios
    # en la asignación de clústers
    while it <= maxit and not all(c == c_new):
        c = np.copy(c_new)
        for i in range(N):
            kmin = 1
            min_dist = float("Inf")
            for k in range(clusters):
                dist = np.linalg.norm(X[i, :] - mu[k, :])
                if dist < min_dist:
                    min_dist = dist
                    kmin = k

            c_new[i] = kmin + 1

        # Actualizar centroides a "Centro de Masa"
        for k in range(1, clusters + 1):
            Xk = X[c_new == k, :]
            mu[k - 1] =  np.sum(Xk, axis=0) / Xk.shape[0]

    return (c, mu, it)

Probemos con el mítico conjunto de datos Iris. Este conjunto de datos básicamente consiste en muestras de distintas plantas iris, donde los atributos medidos son básicamente longitud y ancho de los sépalos y pétalos:

import matplotlib.pyplot as plt
from sklearn.datasets import load_iris


%matplotlib inline

plt.style.use("seaborn")
plt.rcParams["figure.figsize"] = (6, 4)
plt.rcParams["figure.dpi"] = 200

iris_data = load_iris()
plt.scatter(iris_data.data[:, 0], iris_data.data[:, 2], edgecolor="none",
        alpha=0.7, c="k")
plt.xlabel(iris_data.feature_names[0])
plt.ylabel(iris_data.feature_names[2])

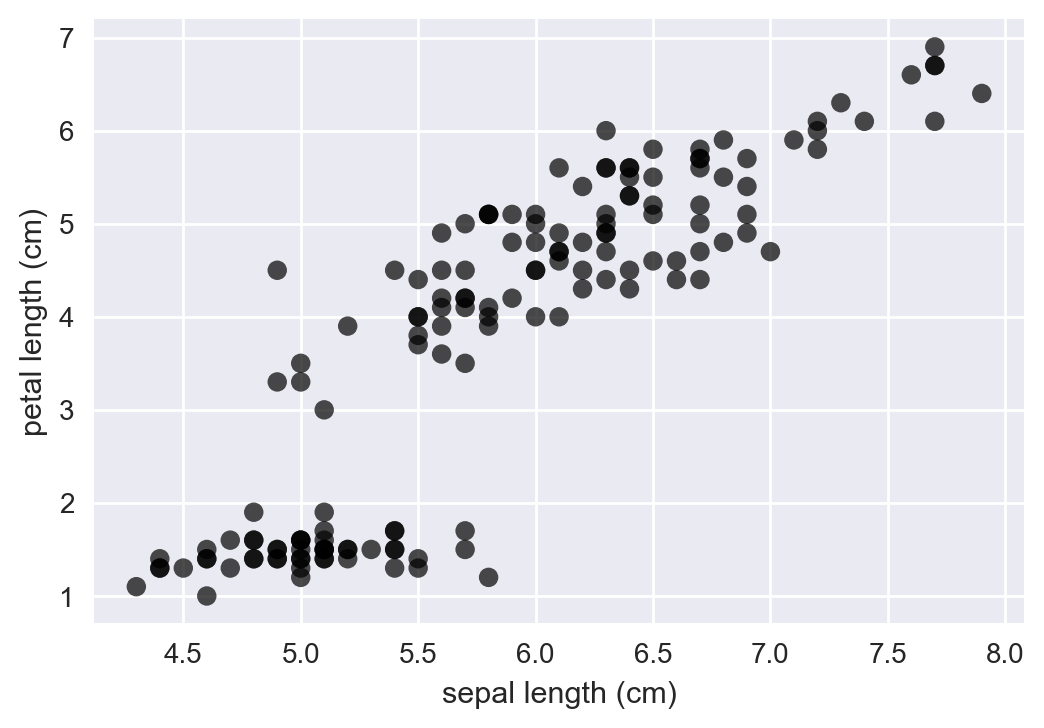
Fig 15: Muestra de datos para el conjunto de datos Iris.

Si aplicaramos el algoritmo descrito con K = 3, ocurriría lo siguiente:

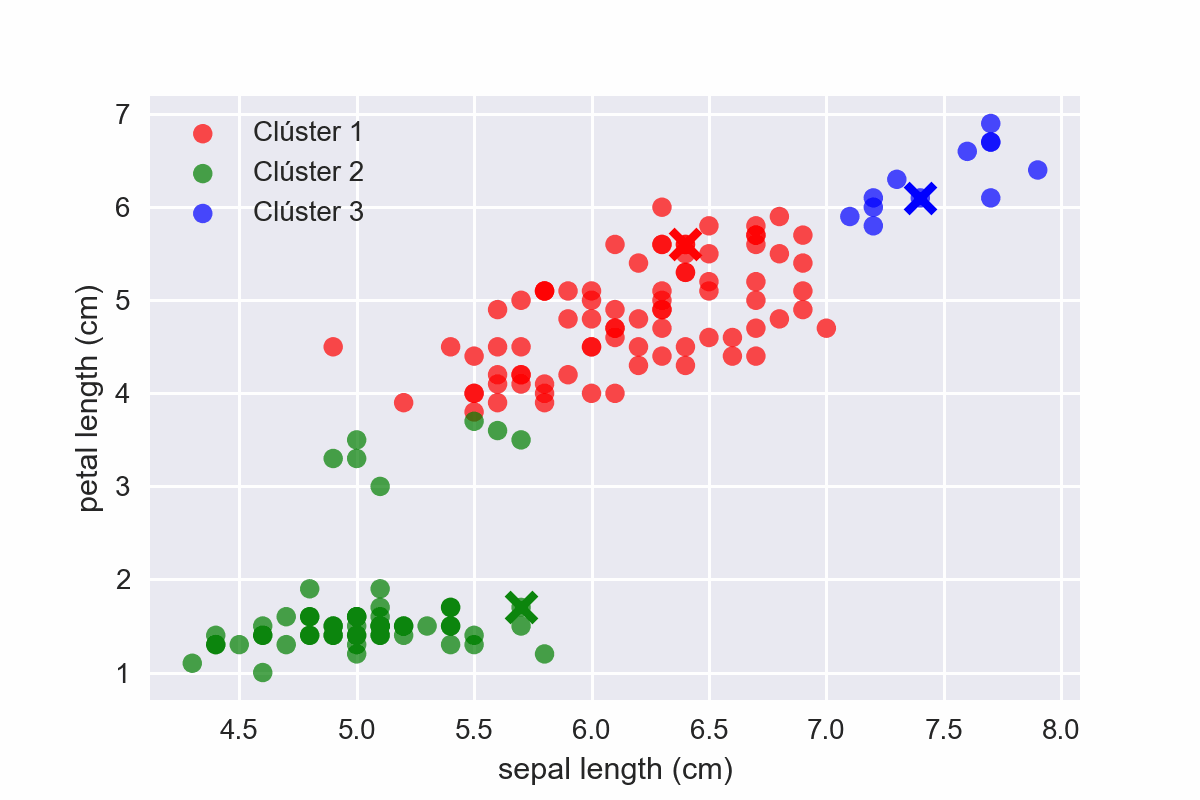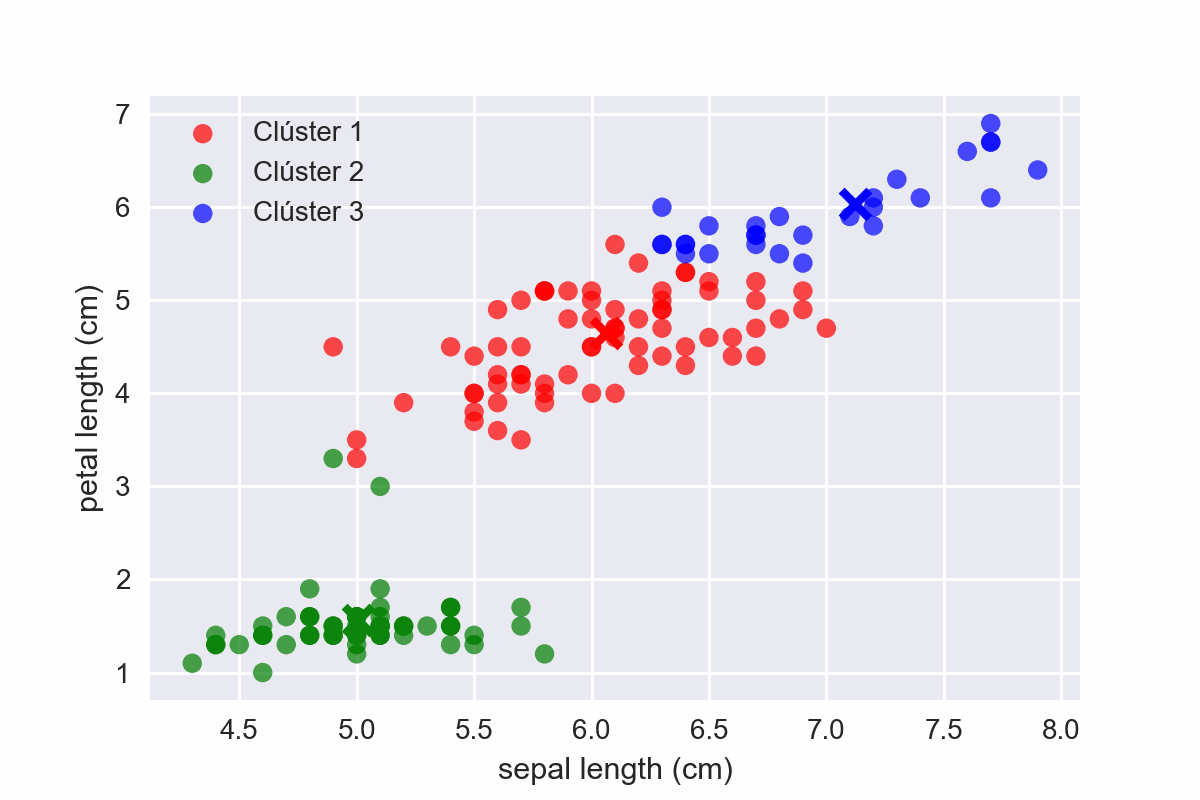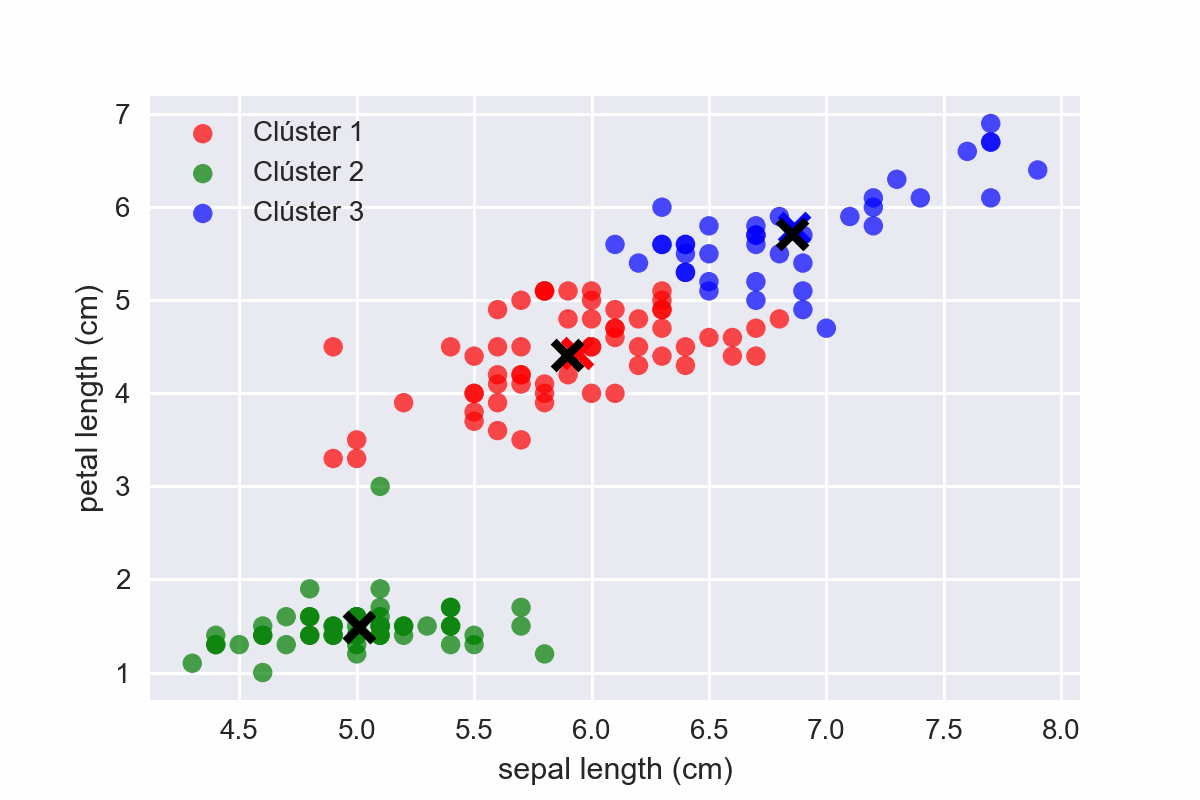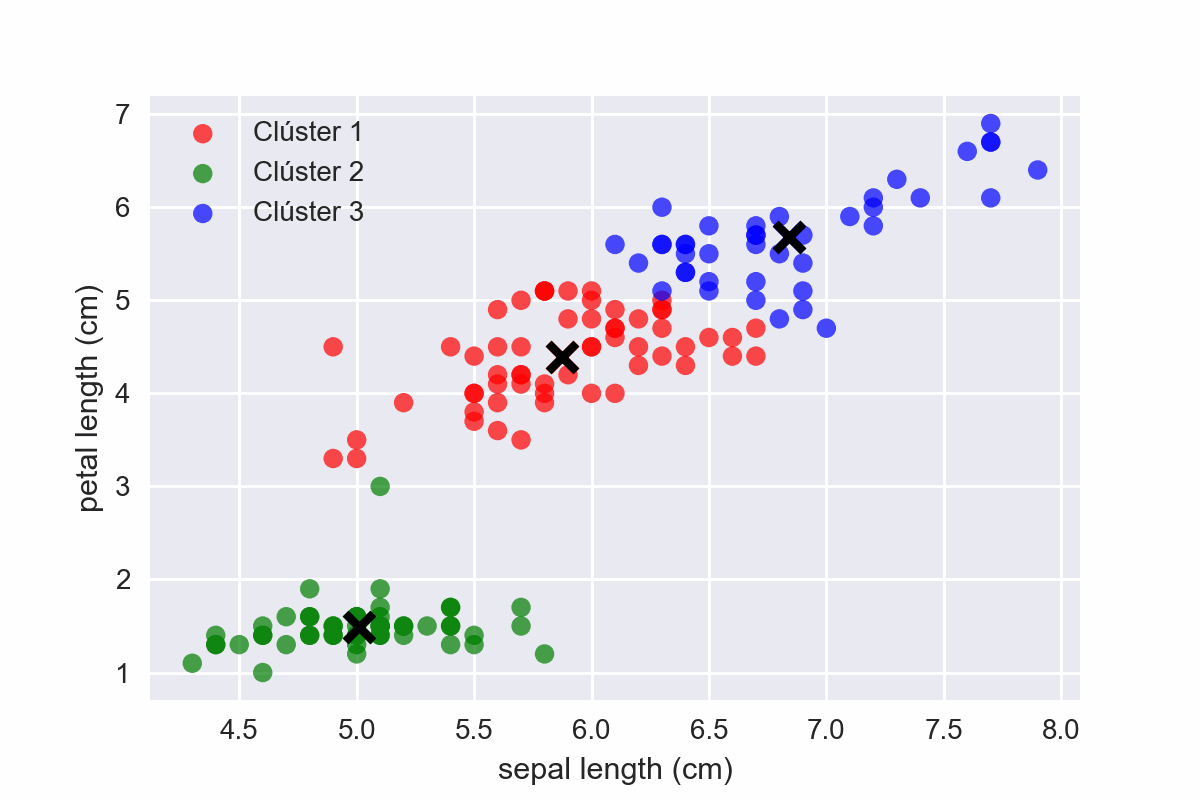
Fig 16: KMeans en acción.

Ahora intentemos darle una interpretación a cada clúster. Consideremos las clases de plantas iris en el conjunto de datos. Para obtener los clústers, utilizaremos la implementación de sklearn:

from sklearn.cluster import KMeans


# Configuramos 3 clústers, para seguir el ejemplo
kmeans = KMeans(n_clusters=3, random_state=0).fit(iris_data.data[:, (0, 2)])

c1 = kmeans.labels_ == 0
c2 = kmeans.labels_ == 1
c3 = kmeans.labels_ == 2

setosa = iris_data.target == 0
versicolor = iris_data.target == 1
virginica = iris_data.target == 2

plt.subplot(121)
plt.scatter(iris_data.data[setosa, 0], iris_data.data[setosa, 2], edgecolor="none",
            alpha=0.7, c="r")

plt.scatter(iris_data.data[versicolor, 0], iris_data.data[versicolor, 2], edgecolor="none",
            alpha=0.7, c="g")

plt.scatter(iris_data.data[virginica, 0], iris_data.data[virginica, 2], edgecolor="none",
            alpha=0.7, c="b")
plt.legend(iris_data.target_names)
plt.xlabel(iris_data.feature_names[0])
plt.ylabel(iris_data.feature_names[2])

plt.subplot(122)
plt.scatter(iris_data.data[c1, 0], iris_data.data[c1, 2], edgecolor="none",
            alpha=0.7, c="m")

plt.scatter(iris_data.data[c2, 0], iris_data.data[c2, 2], edgecolor="none",
            alpha=0.7, c="c")

plt.scatter(iris_data.data[c3, 0], iris_data.data[c3, 2], edgecolor="none",
            alpha=0.7, c="y")
plt.legend(("clúster 1", "clúster 2", "clúster 3"))
plt.xlabel(iris_data.feature_names[0])
plt.ylabel(iris_data.feature_names[2])

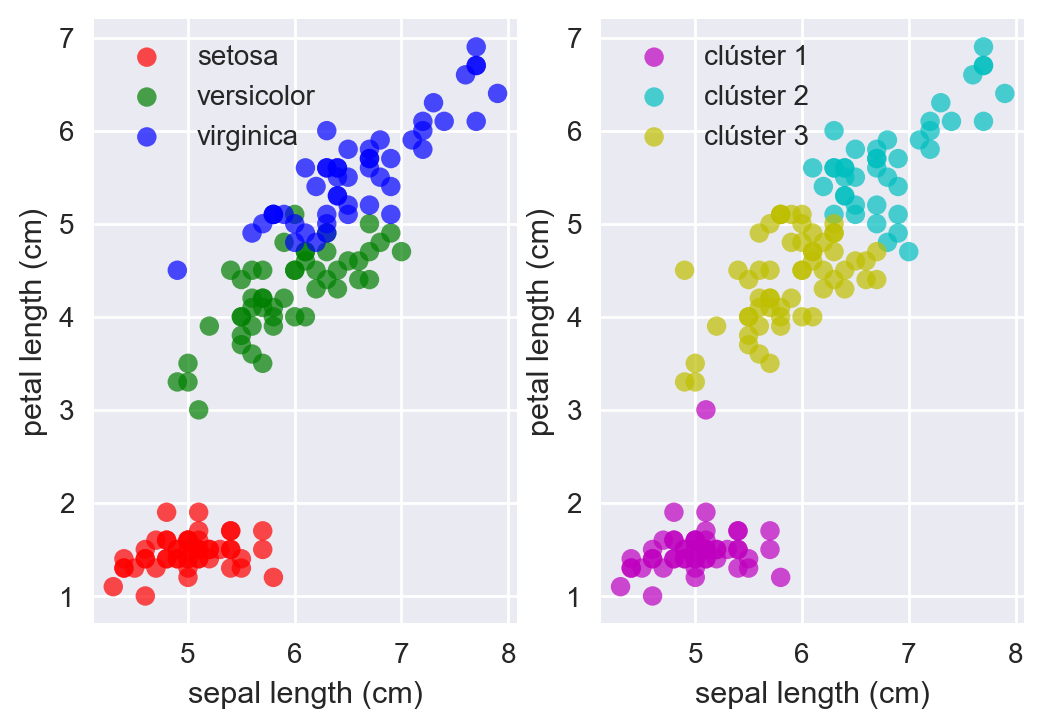
Fig 17: Grupos originales vs Clústers encontrados por KMeans.

En este caso el clúster 1 se puede interpretar como las plantas de clase setosa, el clúster 2 como plantas de clase virginica y el clúster 3 como plantas de clase versicolor.

Observación: En este caso no lo hicimos, ya que los atributos se encontraban en escalas similares, pero, por lo general, al trabajar con clústering, se prefiere escalar los datos, para que no haya un atributo que tenga prioridad sobre otros. Pregunta para pensar ¿Qué pasa cuando consideramos dimensionalidades altas (o a medida que aumentamos la dimensionalidad)?

Otro problema que vemos es que el valor K de la cantidad de clústers es una entrada al algoritmo. Existen métodos para escoger la cantidad de clústers, algunas veces funcionan otras no. Existen otras formas estadísticas también para encontrar la cantidad de clústers, sin embargo, siempre hay que tener en cuenta el contexto ¿mejor considerando qué?. Una forma de encontrar la cantidad de clústers es utilizando el método del codo, en el cual corremos varias veces el algoritmo variando la cantidad de clústers y vemos como varía la inercia de los clústers (básicamente la suma cuadrática de las distancias de cada centroide a cada registro que pertenece al clúster). Escogemos la cantidad de clústers hasta que la variación en la inercia sea casi despreciable (en el gráfico se ve como un codo). Probemos esto para el ejemplo:

N = 10
inertia = np.zeros(N)
n_clusters = np.linspace(1, 10, num=10, dtype=int)
for i, clusters in enumerate(n_clusters):
    inertia[i] = KMeans(
        n_clusters=clusters,
        random_state=1234).fit(iris_data.data[:, (0, 2)]).inertia_

plt.plot(n_clusters, inertia, "o-", color="tomato")
plt.xlabel("Cantidad de clusters")
plt.ylabel("Inercia")
plt.title("Elbow graph")
plt.axvline(3)

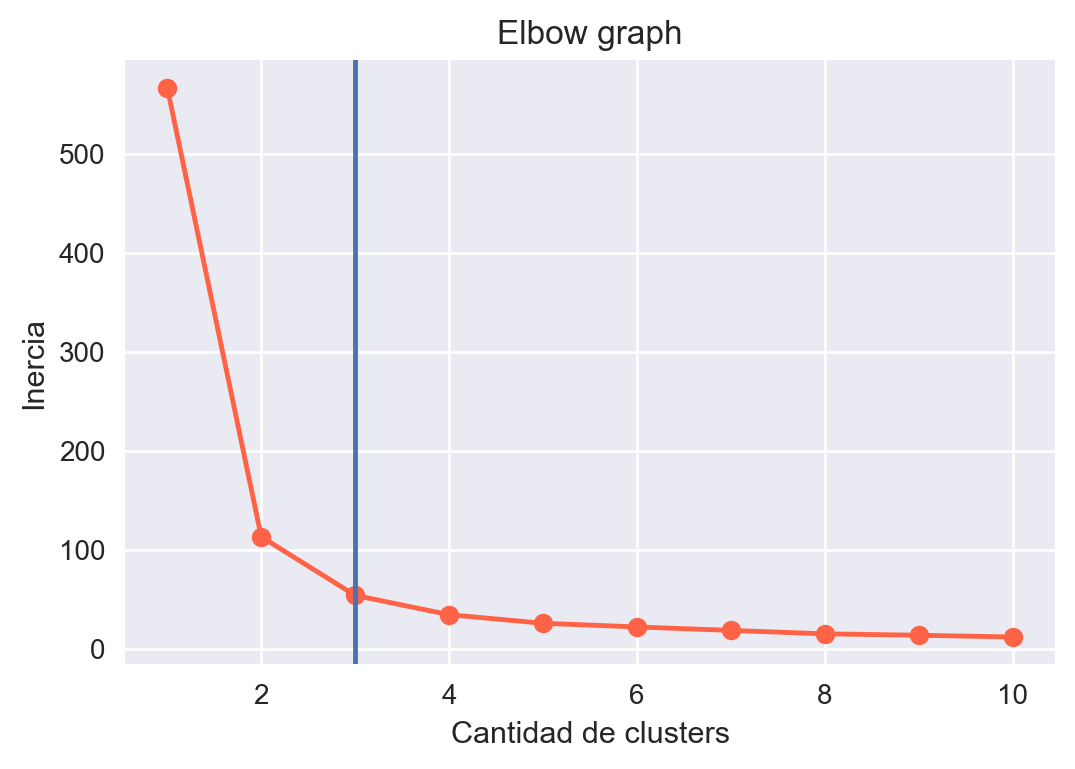
Fig 18: Gráfico de codo.

Para este caso particular, podemos observar que K = 3 es un buen valor para la cantidad de clústers.

Existen otros algoritmos que no requieren conocer la cantidad de clústers apriori (ejemplo: DBScan).

Ejemplo de compresión de imágenes

Como último ejemplo de Kmeans, utilicémoslo para comprimir una imagen. Lo que haremos será hacer clústering, y generar super-píxeles, que serán grupos de pixeles, donde su valor de color será el centroide del clúster. Para el ejemplo, comprimiremos la imagen para que utilice 30 colores, pero ahí pueden ir jugando, teniendo la intuición de que reducir la cantidad de colores, reducirá la calidad de la compresión:

import numpy as np


img = plt.imread("semana7/oso.jpg")
X = img.reshape(img.shape[0] * img.shape[1], img.shape[2])

kmeans = KMeans(n_clusters=30)
kmeans.fit(X)
# Usar centroides para comprimir imagen
X_compressed = kmeans.cluster_centers_[kmeans.labels_]
X_compressed = np.clip(X_compressed.astype("uint8"), 0, 255)

# Re-escalar a dimensiones de imagen original
X_compressed = X_compressed.reshape(img.shape[0], img.shape[1], img.shape[2])

fig, ax = plt.subplots(1, 2, figsize = (12, 8))
ax[0].imshow(img)
ax[0].set_title("Imágen original")
ax[0].axis("off")
ax[1].imshow(X_compressed)
ax[1].set_title("Imagen comprimida con 30 colores")
ax[1].axis("off")

Fig 19: Compresión de imágenes considerando K = 30 K = 10 y K = 5.

Conclusiones

• Se introdujo el concepto de aprendizaje “no supervisado” y algunos ejemplos como reducción dimensional y agrupamiento.
• Se habló de los problemas que pueden surgir cuando se aumenta la dimensionalidad y se habló sobre la maldición de la dimensionalidad, donde se dieron algunas intuiciones.
• Se revisaron técnicas típicas de reducción dimensional tales como análisis factorial y análisis de componentes principales y se mostraron ejemplos prácticos.
• Se introdujo un ejemplo de agrupamiento (clústering), se explicó didácticamente en qué consiste el algoritmo KMeans y se mostró un ejemplo práctico de compresión de imágenes.