¿Consejos? Introducción a las Regresiones
Introducción
Este artículo sigue una estructura similar a mis últimos artículos de la serie De Vuelta a lo Básico, donde expliqué fundamentos de probabilidad, con el fin de transferir conocimiento y hacer que mis otros artículos donde hablo sobre GenAI sean más simples/intuitivos de entender.
Con el objetivo de seguir reciclando el material que alguna vez elaboré para algunas clases, haré una serie de artículos con tópicos clásicos utilizados en “Ciencia de Datos” (odio este término). Este capítulo será una introducción a las regresiones, en particular, la regresión lineal. Sin embargo, debido a preguntas que he recibido de algunos colegas, haré una pequeña sección de “consejos”, lo pongo entre comillas, porque ¿Quién es este pelagato para aconsejar?
Consejos
Lo he mencionado en situaciones anteriores, pero llevo ya dos años trabajando en Meta, ahora recientemente me cambié de equipo. En un post previo Primer año en USA y algunas reflexiones, comenté algunos temas sobre cómo es trabajar en una FAANG (MAANG), y en el caso particular de Meta, cómo es de estresate el proceso de evaluación de desempeño o PSC (buscar stack ranking en dicho post mencionado). En mi primer año, logré estar en el lado derecho de la campana de Gauss (top 1%) y me promovieron de L4 a L5 (rating: Redefined Expectations o RE). Este 2023, en L5, las exigencias y expectativas fueron mucho mayores. En este caso logré estar en el top 15% (rating: Greatly Exceeds Expectations), lo cual me tiene contento porque sacar RE en L5 es muy complicado (hay que tener influencia a nivel multi-organizacional).
Bueno, después de este humble brag, algunos colegas (no muchos la verdad), me preguntaron cómo lo hice para salir tan bien evaluado dos años seguidos. Si bien, no soy nadie para darte la receta del éxito (no existe, y depende de lo que consideres como éxito), las cosas que hice yo en particular fueron:
- Resolver problemas que tuviesen impacto
- Encontrar un buen aliado que entienda bien el negocio
- Investigar y crear soluciones innovadoras (pensar fuera de la caja)
- Reconocer los problemas a resolver, las limitaciones y las prioridades
- Iterar rápido en prototipos y descartar soluciones que no tendrán éxito (luego de $N$ intentos)
- Resetear la mente, y olvidarse de todo lo que sé, en esencia, desafiar mi propio contexto y creencias
- Desafiar el Status Quo a nivel de organización y procesos
- En lo técnico
- Entender rápidamente una base de código y tener impacto lo antes posible
- Ser proficiente en programación. Ejemplo, saber utilizar un debugger (si haces debugging haciendo prints, lo estás haciendo mal)
- Ser capaz de modelar los problemas (ej. con teoría de probabilidad, modelos de teoría de sistemas, etc.)
- Saber bien la teoría y el por qué de las cosas (ej. complejidad asintótica, procesamiento distribuido, modelos de lenguaje, etc.)
No es mucho más lo que hice, creo que no es magia y lo que ayuda es la disciplina y consistencia.
¿Significa esto que no me estreso o no paso sustos? Claro que no, todo lo contrario, me he estresado bastante, creo que es el primer trabajo en el que me estreso para ser honestos. Pero también es el primero en el que no me he aburrido. Ahora en nuevo equipo, con nuevos desafíos, está el miedo, pero bueno, supongo que habrá que ver que ocurre a medida que avanza el año.
Regresión Lineal
En simples términos, consiste en construir un modelo de la relación entre dos o más variables, a partir de datos disponibles. Primero, para ganar una intuición, consideraremos el caso de sólo dos variables, $x$ e $y$ (por ejemplo, años de estudio y sueldo, etc.), y para derivar el modelo, nos basaremos en la colección de pares $(x_i, y_i)$, $i = 1, \ldots, n$. Por ejemplo, $x_i$ podría ser los años de estudio e $y_i$ podría ser los ingresos anuales de la i-ésima persona en la muestra. A menudo un gráfico bi-dimensional de estas muestras indica una una relación lineal aproximada entre la relación de $x_i$ e $y_i$. Luego, es natural intentar construir un modelo lineal de la forma:
$$y \approx \theta_0 + \theta_1 x$$
Donde $\theta_0$ y $\theta_1$ son parámetros desconocidos que deberán ser estimados. En particular, dados los estimados $\hat{\theta}_0$ y $\hat{\theta}_1$ de los parámetros, el valor de $y_i$ correspondiente a $x_i$, predecido por el modelo, es:
$$\hat{y}_i = \hat{\theta}_0 + \hat{\theta}_1x_i$$
Por lo general, $\hat{y}_i$ será diferente del valor de $y_i$, y la diferencia correspondiente:
$$\tilde{y}_i = y_i - \hat{y}_i$$
se le llama el i-ésimo residual. Elegir los estimadores que resulten en valores pequeños para los residuales se considera que proveen un buen ajuste a los datos. Utilizando esto como motivador, el enfoque de regresión lineal escoge parámetros estimados $\hat{\theta}_0$ y $\hat{\theta}_1$ que minimicen la suma de los residuales al cuadrado:
$$\sum_{i=1}^{n} (y_i - \hat{y}_i)^2 = \sum_{i=1}^{n} (y_i - \theta_0 - \theta_1 x_i)^2$$
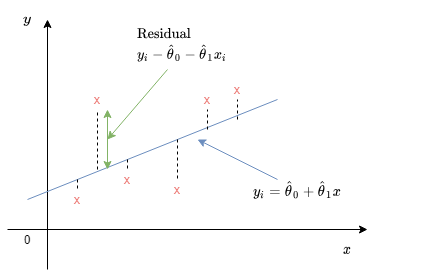
Fig 1: Visualización de un modelo lineal.
Notar que el modelo lineal sugerido podría ser verdadero o no. Por ejemplo, la relación real entre las variables podría ser no lineal. El enfoque de mínimizar los residuales al cuadrado intenta encontrar el mejor modelo lineal posible, e involucra una hipótesis implícita que la relación entre las variables es lineal y que es válida.
Para derivar las fórmulas para las estimaciones $\hat{\theta}_0$ y $\hat{\theta}_1$, observamos que una vez se tienen los datos, la suma de los residuales al cuadrado es una función cuadrática de $\hat{\theta}_0$ y $\hat{\theta}_1$. Para minimizar la suma cuadrática $S$ de los residuales, calculamos las derivadas parciales con respecto a $\theta_0$ y $\hat{\theta}_1$ y las igualamos a 0 (punto crítico, mínimo de la función, no entraremos en detalle respecto a esto):
$$\frac{\partial S}{\partial \theta_0} = -2 \sum_{i=1}^{n} (y_i - \theta_0 - \theta_1x_i) = 0$$
$$\frac{\partial S}{\partial \theta_1} = -2 \sum_{i=1}^{n} (y_i - \theta_0 - \theta_1x_i)x_i = 0$$
Resolviendo para $\theta_0$:
$$ \begin{array}{ll} 0 & = \sum_{i=1}^{n} (y_i - \hat\theta_0 - \hat\theta_1x_i)\\ \sum_{i=0}^{n}\theta_0 & = \sum_{i=1}^{n} (y_i - \hat\theta_1x_i)\\ n\hat\theta_0 & = \sum_{i=1}^{n} y_i - \hat\theta_1 \sum_{i=1}^{n} x_i\\ \hat\theta_0 & = \bar{y} - \hat\theta_1 \bar{x} \end{array} $$
Resolviendo para $\theta_1$:
$$ \begin{array}{ll} 0 & = \sum_{i=1}^{n} (y_i - \hat\theta_0 - \hat\theta_1x_i)x_i\\ 0 & = \sum_{i=1}^{n} (y_i - \bar{y} + \hat\theta_1 \bar{x} - \hat\theta_1x_i)x_i\\ \hat\theta_1 &= \frac{\sum_{i=1}^{n} (y_i - \bar{y})x_i}{\sum_{i=1}^{n} (x_i - \bar{x})x_i} \end{array} $$
Con el siguiente desarrollo algebraico (un poco tedioso, uff):
$$ \begin{array}{ll} \sum_{i=1}^{n} (y_i - \bar{y})x_i & = (y_1 - \bar{y})x_1 + \ldots + (y_n - \bar{y})x_n \\ & = (y_1 - \frac{1}{n}(y_1 + \ldots + y_n))x_1 + \ldots + (y_n - \frac{1}{n}(y_1 + \ldots + y_n))x_n \\ & = y_1x_1 - \frac{y_1x_1}{n} - \frac{y_2x_1}{n} - \ldots -\frac{y_nx_1}{n} \\ & \quad \vdots \\ & \quad y_nx_n - \frac{y_1x_n}{n} - \frac{y_2x_n}{n} - \ldots -\frac{y_nx_n}{n} \\ & = x_1y_1 + \ldots + x_ny_n - y_1\bar{x} - \ldots - y_n\bar{x} \\ & = \sum_{i=1}^{n} x_iy_i - y_i\bar{x} \\ \end{array} $$
Tomando parte de la ecuación, también se puede obtener:
$$ \begin{array}{ll} x_1y_1 + \ldots + x_ny_n - y_1\bar{x} - \ldots - y_n\bar{x} & = x_1y_1 + \ldots + x_ny_n - \bar{x} (y_1 + \ldots + y_n) \\ &= x_1y_1 - \bar{x}\bar{y} + \ldots + x_ny_n - \bar{x}\bar{y} \\ &= \sum_{i=1}^{n} x_iy_i - \bar{x}\bar{y} \end{array} $$
De las 3 formas de escribir el numerador, llegamos a que:
$$\bar{x}\bar{y} = x_i\bar{y} = y_i\bar{x}$$
Ahora, haciendo una “Harry-Potteada”, o sea literalmente magia a la expresión del numerador de $\hat\theta_1$:
$$ \begin{array}{ll} \sum_{i=1}^{n} (y_i - \bar{y})x_i & = \sum_{i=1}^{n} x_iy_i - x_i\bar{y} \\ & = \sum_{i=1}^{n} x_iy_i - \bar{x}\bar{y} \\ & = \sum_{i=1}^{n} x_iy_i - \bar{x}\bar{y} - \bar{x}\bar{y} + \bar{x}\bar{y} \\ & = \sum_{i=1}^{n} x_iy_i - x_i\bar{y} - y_i\bar{x} + \bar{x}\bar{y} \\ & = \sum_{i=1}^{n} (y_i - \bar{y})(x_i - \bar{x}) \end{array} $$
Procediendo de forma similar en el denominador, se llega a una expresión equivalente para $\hat{\theta_1}$:
$$\hat\theta_1 = \frac{\sum_{i=1}^{n} (y_i - \bar{y})(x_i - \bar{x})}{\sum_{i=1}^{n} (x_i - \bar{x})^2}$$
Se parece a la fórmula de correlación ¿o no? Es sutilmente diferente, pues el numerador podría verse como la covarianza entre $x$ e $y$, y el denominador como la varianza de $x$.
Ejemplo: A través del tiempo, la torre de Pisa tiende a inclinarse. Algunas mediciones entre los años 1975 y 1987 de la distancia de un punto fijo de la torre, respecto a su posición si la torre estuviese derecha producen la siguiente tabla:
| Año | Inclinación |
|---|---|
| 1975 | 2.9642 |
| 1976 | 2.9644 |
| 1977 | 2.9656 |
| 1978 | 2.9667 |
| 1979 | 2.9673 |
| 1980 | 2.9688 |
| 1981 | 2.9696 |
| 1982 | 2.9698 |
| 1983 | 2.9713 |
| 1984 | 2.9717 |
| 1985 | 2.9725 |
| 1986 | 2.9742 |
| 1987 | 2.9757 |
Probemos las ecuaciones descritas, en el siguiente código python intentamos ajustar los datos a un modelo lineal.
import matplotlib.pyplot as plt
import numpy as np
%matplotlib inline
plt.style.use("seaborn")
plt.rcParams["figure.figsize"] = (6,4)
plt.rcParams["figure.dpi"] = 200
x = np.array([1975, 1976, 1977, 1978, 1979, 1980, 1981, 1982, 1983, 1984, 1985, 1986, 1987])
y = np.array([2.9642, 2.9644, 2.9656, 2.9667, 2.9673, 2.9688, 2.9696, 2.9698, 2.9713, 2.9717, 2.9725, 2.9742, 2.9757])
num = sum((x[i] - np.mean(x))*(y[i] - np.mean(y)) for i in range(len(x)))
den = sum((x[i] - np.mean(x))**2 for i in range(len(x)))
theta_1_est = num/den
theta_0_est = np.mean(y) - np.mean(x)*theta_1_est
plt.plot(x, y, "r.")
xx = np.linspace(1975, 1987)
yy = theta_0_est + theta_1_est*xx
plt.plot(xx, yy, "b-")
Lo que entrega como resultado:
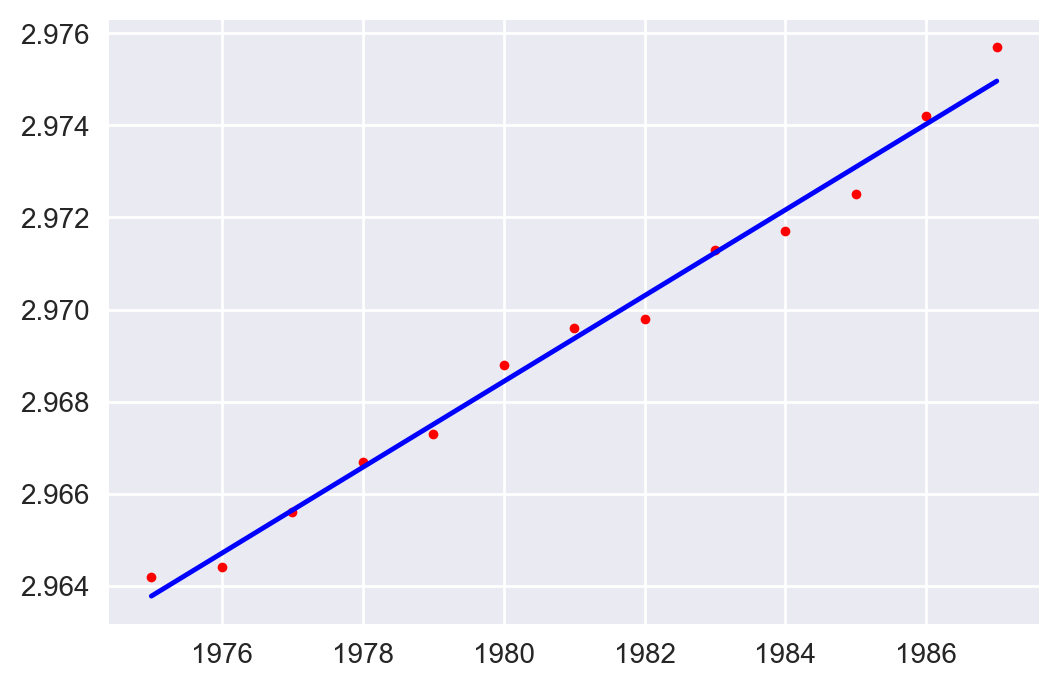
Fig 2: Ejemplo de inclinación de la torre de Pisa.
Justificación de la formulación por mínimos cuadrados
Asumimos que $x_i$ son números (no variables aleatorias). Asumimos que $y_i$ es la realización de una variable aleatoria $Y_i$, generada de acuerdo a la ecuación:
$$Y_i = \theta_0 + \theta_1 x_i + W_i \quad i = 1, \ldots, n$$
donde $W_i$ (ruido) son variables aleatorias normales independientes e idénticamente distribuidas (i.i.d) con media 0 y varianza $\sigma^2$. Siguiendo este razonamiento, se tiene que $Y_i$ son variables normales e independientes, donde $Y_i$ tiene media $\theta_0 + \theta_1 x_i$ y varianza $\sigma^2$. La función de probabilidad toma la forma:
$$f_Y(y;\theta) = \prod_{i=1}^{n} \frac{1}{\sqrt{2\pi}\sigma} e^{-\frac{(y_i - \theta_0 - \theta_1 x_i)^2}{2\sigma^2}}$$
Maximizar la función de probabilidad es lo mismo que maximizar el exponente en la expresión de arriba, lo que es equivalente a minimizar la suma cuadrática de los residuales. Así, las estimaciones de la regresión lineal pueden verse como estimaciones de máxima probabilidad en un contexto lineal adecuado. De hecho, dado algunos supuestos (que mencionaremos más adelante), puede demostrarse que en este contexto los estimadores son insesgados.
Regresión Lineal Múltiple
Hasta ahora, hemos hablado de regresiones que involucran solo una variable explicativa, digamos $x$, este es un caso especial conocido como regresión lineal simple. El objetivo consistió en construir un modelo que explica los valores observados $y_i$ a partir de los valores $x_i$. Sin embargo, muchos fenómenos involucran múltiples variables explicarivas o latentes (ejemplo, un modelo que intente estimar el ingreso anual a partir de los años de estudio y la edad). Modelos de este tipo se conocen como modelos de regresión múltiple.
Por ejemplo, supongamos que los datos consisten en triplets de la forma $(x_i, y_i, z_i)$ y que queremos estimar los parámetros $\theta_j$ de un modelo con forma:
$$y \approx \theta_0 + \theta_1 x + \theta_2 z$$
Por ejemplo, $y_i$ podría ser el ingreso anual, $x_i$ podría ser la edad y $z_i$ los años de estudio, de la i-ésima persona en una muestra aleatoria. Entonces, buscamos minimizar la suma de los residuales al cuadrado:
$$\sum_{i=1}^{n} (y_i - \theta_0 - \theta_1 x_i - \theta_2 z_i)^2$$
De forma general, no hay límite en la cantidad de variables explicarivas a utilizar. El cálculo de las estimaciones $\hat \theta_i$ de la regresión es conceptualmente el mismo que en el caso de una sola variable explicativa, pero por supuesto, las fórmulas se vuelven un poco más complejas.
También existe el caso especial en que $z_i = x_i^2$, en el cual estamos lidiando con un modelo de la forma:
$$y \approx \theta_0 + \theta_1 x + \theta_2 x^2$$
Dicho modelo sería apropiado si existe una buena razón para esperar una relación cuadrádica entre $y_i$ y $x_i$ (También podrían utilizarse modelos polinomiales de mayor grado). A pesar de que dicha dependencia cuadrática es no lineal, seguimos diciendo que el modelo latente es lineal, en el sentido de que los parámetros desconocidos $\hat \theta_j$ están relacionados linealmente con las variables aleatorias observadas $Y_i$. De forma general, podríamos tener modelos de la forma:
$$y \approx \theta_0 + \sum_{j=1}^{m} \theta_j h_j(x)$$
Donde $h_j$ podría ser cualquier función que capture la dependencia anticipada de $y$ en $x$. Finalmente, para obtener las estimaciones de los parámetros, se puede proceder de la misma forma (mínimos cuadrados), y para ello existen métodos numéricos eficientes.
Para seguir la notación comúnmente vista en la literatura, consideraremos el modelo de regresión lineal múltiple:
$$y_i = \beta_0 + \beta_1 X_1 + \beta_2 X_2 + \ldots + \beta_n X_n + \varepsilon_i$$
Donde $\beta_i$ ($i = 1, \ldots, n$) son los coeficientes de la regresión, y $\beta_0$ se conoce como el intercepto. El término $\varepsilon_i$ es un término de error. Recordemos que para obtener las estimaciones de los parámetros del modelo lineal latente, minimizamos la suma cuadrática de los residuales (OLS: Ordinary Least Squares). Se dice la estimación lineal es ELIO (Estimador Lineal Insesgado Óptimo), si se cumplen los supuestos de Gauss-Markov.
El teorema de Gauss-Markov enuncia que si un modelo de regresión satisface los 6 primeros supuestos clásicos, entonces la regresión OLS produce estimadores insesgados que tienen la menor varianza entre todos los posibles estimadores; en palabras simples, se obtiene un estimador óptimo. Los supuestos son los siguientes:
- El modelo de regresión es lineal en los coeficientes y el término de error $\varepsilon$
- El término de error tiene una población de media 0. (Si se considera el término constante en el modelo, este supuesto se cumple ya que esta constante fuerza que el promedio de los residuales sea 0).
- Todas las variables independientes (regresores) no tienen correlación con el término de error (exogeneidad).
- Las obervaciones del término de error no tienen correlación entre ellas.
- El término de error tiene varianza constante (homocedasticidad).
- No hay variable independiente que sea una combinación lineal perfecta de otras variables.
- Opcional: El término de error está normalmente distribuido.
Ejemplo Práctico
Para tener un mejor entendimiento de las ideas planteadas, desarrollaremos un ejemplo práctico en python. Para ello, consideraremos los mismos datos del ejemplo de la torre de Pisa (ver tabla más arriba).
import matplotlib.pyplot as plt
import numpy as np
import pandas as pd
%matplotlib inline
plt.style.use("seaborn")
plt.rcParams["figure.figsize"] = (6,4)
plt.rcParams["figure.dpi"] = 200
data = pd.DataFrame({
"year": np.array([
1975,
1976,
1977,
1978,
1979,
1980,
1981,
1982,
1983,
1984,
1985,
1986,
1987
]),
"lean": np.array([
2.9642,
2.9644,
2.9656,
2.9667,
2.9673,
2.9688,
2.9696,
2.9698,
2.9713,
2.9717,
2.9725,
2.9742,
2.9757
])
})
Ajustemos un modelo lineal utilizando la biblioteca statsmodels:
import statsmodels.api as sm
import statsmodels.formula.api as smf
model = smf.ols("lean ~ year", data)
fitted_model = model.fit()
fitted_model.summary()
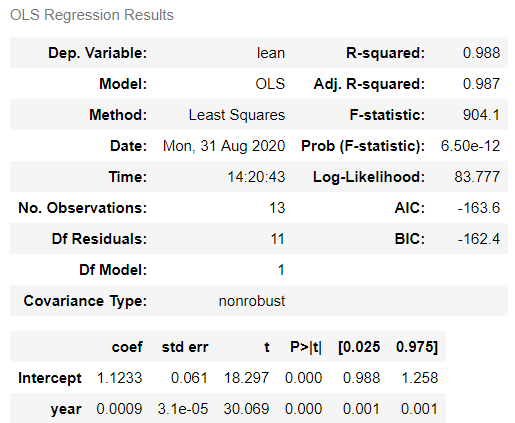
Fig 4: Resultados de ajuste OLS.
Los resultados muestran que fuimos consistentes con la derivación hecha más arriba, ya que obtuvimos los mismos valores para los parámetros. También es interesante detallar cómo interpretar cada uno de los valores entregados en los resultados:
-
F-value: Es una prueba de hipótesis, cuya hipótesis nula es Todos los coeficientes son 0, o en otras palabras que el modelo no tiene capacidad predictiva. Idealmente esperamos que este valor sea alto (mucho mayor que 1), y que elp-valuesea pequeño, para tener un nivel de significancia estadística deseable (ej. menor que 0.05) -
DF residuals: Grados de libertad y se calcula como el tamaño muestral menos la cantidad de parámetros. En este caso da 11, pues se cuenta con 13 observaciones y dos parámetros. -
R-squared: Es el procentaje de varianza explicado por los datos. Va entre 0 a 1, e idealmente queremos que esté cercano a 1. -
Adj. R-squared: Es el valor ajustado de la estadística anterior. Este se utiliza, debido a que a medida que aumenta la cantidad de predictores, tiende a “inflarse” el valor deR-squaredno necesariamente logrando un modelo mejor o útil. Este valor se calcula básicamente considerando significancia en la mejora de la métrica, a medida que se agregan predictores. -
t: Básicamente es el valor del coeficiente dividido por el error estándar. En esencia, mientras mayor el valor de esta métrica, menor error estándar, por lo que idealmente queremos que esté valor sea grande.
Ahora, analicemos cada uno de los supuestos, enunciados anteriormente. El primer supuesto se cumple, ya que estamos ajustando un modelo lineal. El supuesto 2, también se cumple, pues el modelo está considerando un valor para el intercepto, si calculamos el promedio de los residuales, observamos que es cercano a 0:
predictions = fitted_model.predict(data["year"])
residuals = predictions - data["lean"]
np.mean(residuals)
-2.445906725020345e-14
Para el supuesto 3, podemos calcular la correlación entre los regresores y los residuales, en este caso podemos hacer data["year"].corr(residuals), lo que nos entrega -4.984594328929679e-13, que es cercano a 0, por lo que es seguro decir que no hay correlación entre el regresor y los residuales.
Ahora veamos los supuestos 4 y 5. Para ello graficaremos los residuales, y veremos si existe alguna correlación entre ellos; para el supuesto 4, graficaremos los residuales en función de las predicciones, para ver si la varianza de las predicciones es constante:
plt.figure()
plt.plot(residuals, "go-")
plt.hlines(y=0, xmin=0, xmax=data.shape[0], linestyles="dashed")
plt.xlabel("Orden Observaciones")
plt.ylabel("Residual")
plt.figure()
plt.plot(predictions, residuals, "bo")
plt.hlines(y=0, xmin=np.min(predictions), xmax=np.max(predictions), linestyles="dashed")
plt.xlabel("Predicciones")
plt.ylabel("Residual")
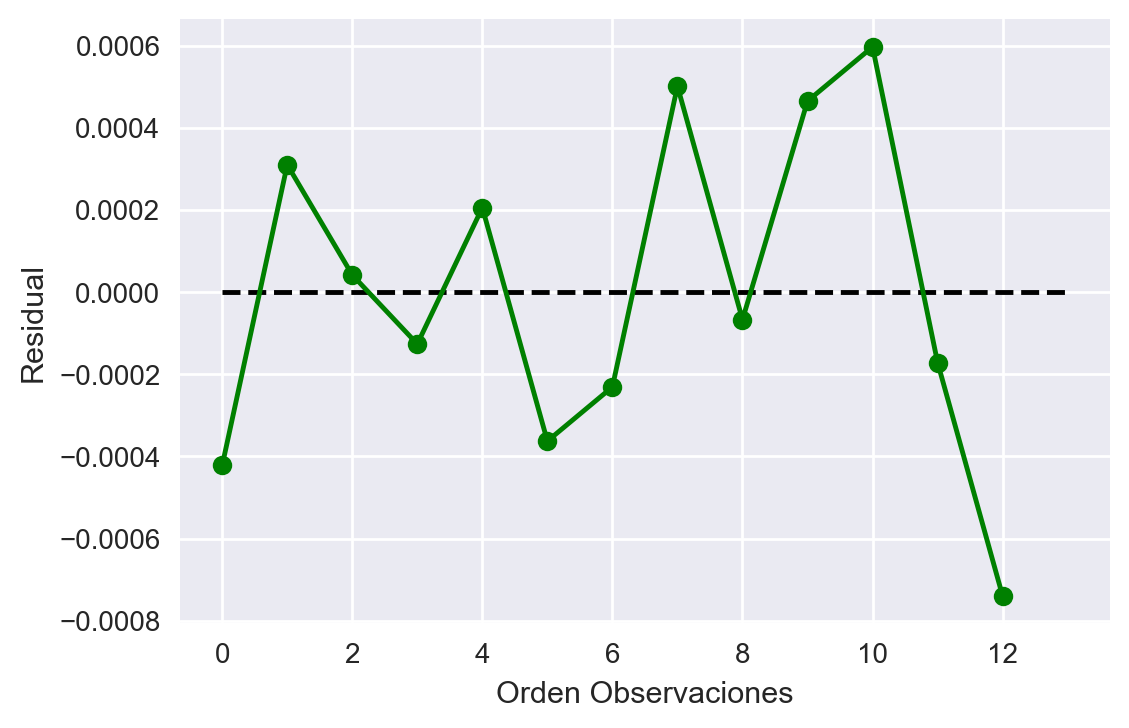
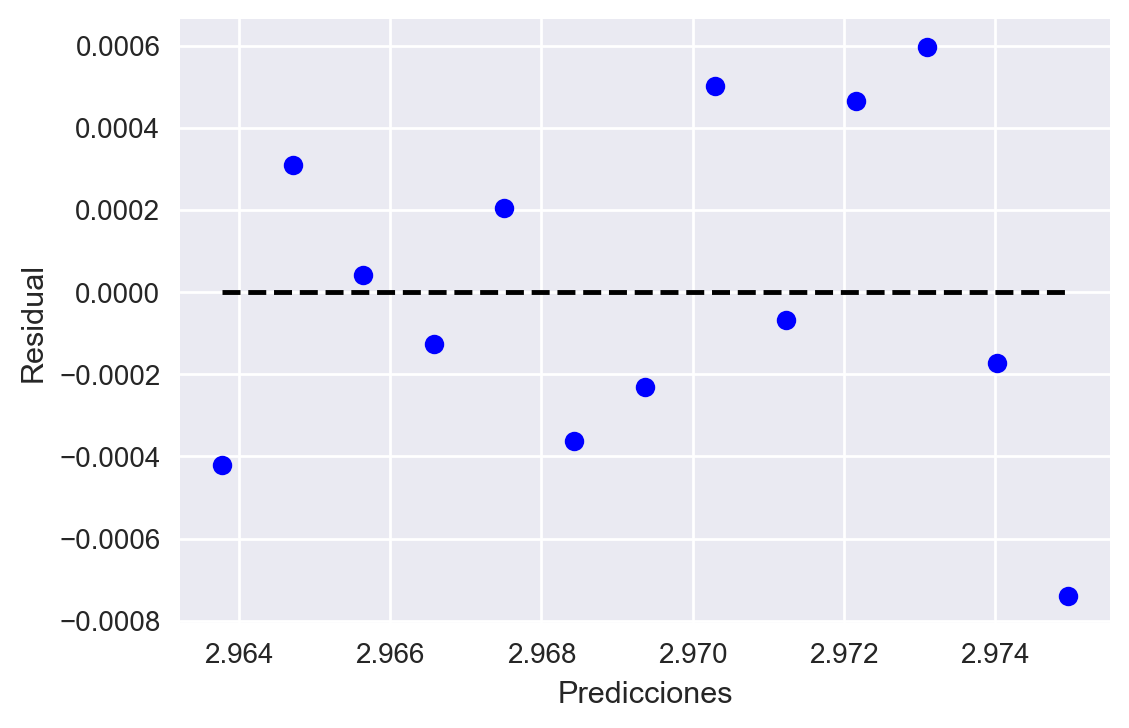
Fig 4: Supuestos 4 y 5 de Gauss-Markov.
De los gráficos observamos que no existe una tendencia clara en los residuales (no se ve correlación entre ellos), además, la varianza en las predicciones se mantiene aproximadamente constante.
Para el supuesto 6, no aplica en este caso ya que sólo tenemos un regresor. En el caso de que hayan dos regresores que sea combinación lineal de otro (ej. tiempo en segundos, tiempo en minutos), básicamente cualquier solver de OLS, arrojará error. Lo que ocurririá es que no se podría diferenciar un regresor de otro (puede que contengan la misma información).
Una vista desde el Aprendizaje Automático (Machine Learning)
En general, en estudios de diversas índoles, se utilizan modelos de regresión lineal para extraer ciertas propiedades de poblaciones y analizarrelaciones entre regresores y la variable dependiente. Por otro lado, el enfoque del aprendizaje automático es usualmente generar modelos predictivos que sean generalizables (que tengan buen rendimiento en la práctica). Antes de poner en producción un modelo predictivo, es necesario intentar estimar el error esperado fuera de muestra, esto es, el error que se espera que tendrá el modelo una vez puesto en producción. De esta forma, se evita tener sobre-ajuste (overfitting), es decir, que el modelo funciona bien sólo en los datos a disposición, pero no es capaz de generalizar a datos nuevos. Un enfoque para estimar el error esperado fuera de muestra, es dividir el conjunto de datos en dos, un conjunto de entrenamiento y uno de validación. En general, la proporción dependerá de la distribución de los datos y de la disposición de ellos, pero valores típicos utilizados son 80%, 20% o 2/3;1/3.
El intercambio de sesgo y varianza (bias variance tradeoff)
Esto no es particular del aprendizaje automático, si no que es una consecuencia de estimación de parámetros (que vimos la semana pasada). Repasemos un poco esto, ya que nos servirá para ganar intuiciones y conectar contenidos. Primero recordemos la fórmula de la varianza:
$$ \begin{array}{ll} var(X) & = E[(X - E[X])^2]\\ & = E[X^2 - 2(E[X])^2 + (E[X])^2] \\ & = E[X^2] - 2E[X]^2 + E[X]^2 \\ & = E[X^2] - (E[X])^2 \end{array} $$
Ahora, recordemos el error de estimación $\tilde \Theta_n = \hat \Theta_n - \theta$, donde $\hat \Theta_n$ es nuestro estimador del parámetro $\theta$. Ahora recordemos el sesgo del estimador, que es el error esperado del error de estimación, es decir:
$$b_{\theta}(\hat \Theta_n) = E[\tilde \Theta_n] = E[\hat \Theta_n - \theta]$$
Finalmente, consideremos la varianza del error de estimación:
$$ \begin{array}{ll} var_{\theta}(\tilde \Theta_n) & = E[\tilde \Theta_n^2] - (E[\tilde \Theta_n^2])^2\\ var_{\theta}(\hat \Theta_n - \theta) & = E[\tilde \Theta_n^2] - b_{\theta}(\hat \Theta_n)^2\\ E[\tilde \Theta_n^2] &= b_{\theta}^2(\hat \Theta_n) + var_{\theta}(\hat \Theta_n) \end{array} $$
Por lo que obtenemos el error cuadrático de la estimación $E[\tilde \Theta_n^2]$ depende del sesgo del estimador $ b_{\theta}(\hat \Theta_n)^2$ y de la varianza $var_{\theta}(\hat \Theta_n)$, por lo que por lo general, existirá un intercambio entre estas dos propiedades, con el fin de reducir el error esperado. Cabe destacar que un buen estimador por lo general tiene bajo sesgo y baja varianza.
Ejemplo Completo
A modo de ejemplo, consideremos que tenemos una cierta muestra de datos con ruido (donde sabemos que el modelo real es y = 2*x. Consideremos la siguiente muestra (usamos random seed por reproducibilidad). Vamos a considerar dos modelos, el primero es un modelo lineal simple, y el segundo será un modelo polinomial (dato freak, una forma de obtener un polinomio de interpolación de N puntos es considerar ajustar los datos a un polinomio de grado N - 1; Teorema de existencia y unicidad del polinomio de interpolación):
from sklearn.linear_model import LinearRegression
from sklearn.model_selection import train_test_split
np.random.seed(40)
# Generar datos de entrenamiento
X = np.linspace(0, 20, num=30)
# Agregamos ruido gaussiano a los datos para hacerlo más interesante
y = 2*(X + np.random.normal(0, 1, len(X)))
# Separar en conjunto de prueba y validación
X_train, X_test, y_train, y_test = train_test_split(
X, y, test_size=0.33, random_state=42)
model_1 = LinearRegression()
# Usamos reshape porque tenemos sólo una columna
model_1.fit(X_train.reshape(-1, 1), y_train)
# Ajustar a un polinomio de grado N-1 (interpolar todos los puntos)
X_train_poly = np.vander(X_train, len(X_train))
coeff = np.linalg.solve(X_train_poly, y_train)
Ahora calculemos el error dentro de la muestra, de nuestros modelos ajustados:
from sklearn.metrics import mean_squared_error
# Calculamos error dentro de muestra
y_pred_model_1 = model_1.predict(X_train.reshape(-1, 1))
y_pred_model_2 = np.dot(X_train_poly, coeff)
print(f"Modelo 1: MSE: {mean_squared_error(y_train, y_pred_model_1)}")
print(f"Modelo 2: MSE: {mean_squared_error(y_train, y_pred_model_2)}")
Modelo 1: MSE: 3.4803735743330284
Modelo 2: MSE: 0.0030419521258808397
Observamos que como era de esperarse, el modelo polinomial ajusta perfectamente el conjunto de datos (error casi 0), mientras que el modelo lineal, tiene cierto sesgo en las estimaciones. Ahora grafiquemos los datos y los modelos obtenidos:
xx = np.linspace(0, 20, num=1000)
yy_model_1 = model_1.predict(xx.reshape(-1, 1))
yy_model_2 = np.dot(np.vander(xx, len(X_train)), coeff)
plt.plot(xx, yy_model_1, "k-")
plt.plot(xx, yy_model_2, "b-")
plt.plot(X_train, y_train, "r.")
plt.plot(X_test, y_test, "g.")
plt.legend(("Modelo Lineal",
f"Modelo Polinomial de Grado {len(X_train) - 1}",
"Datos Entrenamiento",
"Datos Validación"), loc="upper center")
plt.ylim(-10, 50)
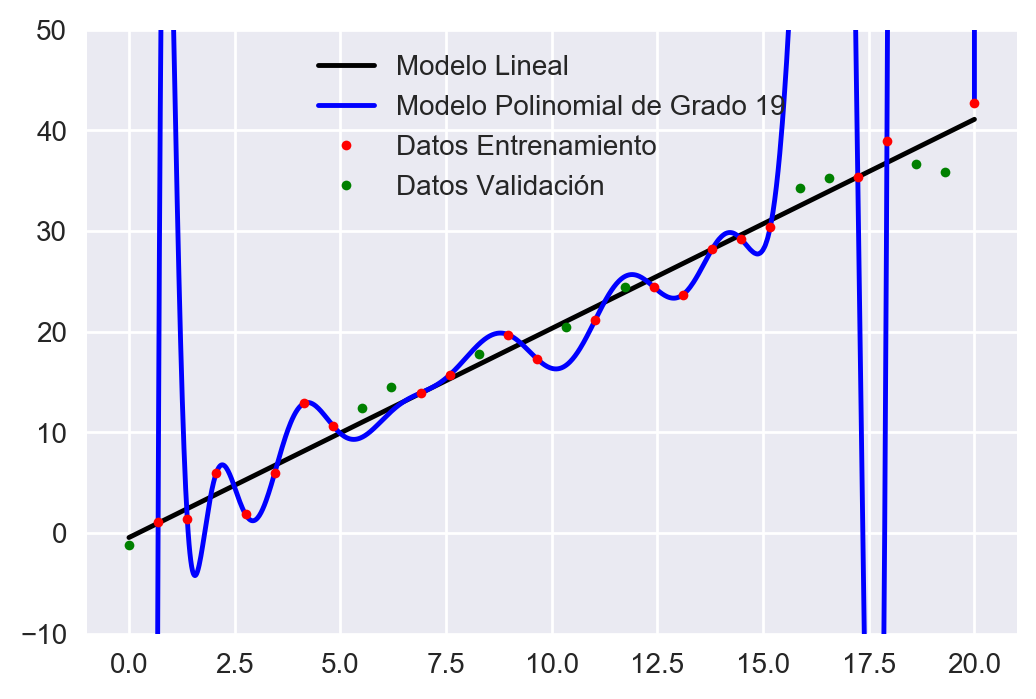
Fig 5: Ejemplo Sobre-ajuste de modelo.
¡Whoa! ¿Qué pasó aquí? Vemos que el modelo 2 (polinomio), en efecto pasa por todos los puntos del conjunto de entrenamiento. Sin embargo, ¡se equivoca garrafalmente en el conjunto de validación! Una forma de visualizar esto, es que básicamente la “máquina” se aprendió los datos de memoria, y no fue capaz de generalizar (esto se conoce como sobre-ajuste o overfit). Una analogía, es por ejemplo un estudiante que se aprende un cuestionario de memoria, o un conjunto de ejercicios de cálculo de memoria. Si el estudiante no es capaz de generalizar, y la prueba consiste en preguntas sutilmente diferentes al cuestionario/listado de ejercicios, es muy probable que el estudiante que memorizó, no pueda generalizar y por lo tanto no tenga un buen rendimiento en la prueba. Finalmente, calculemos el error de validación (estimación del error fuera de muestra):
X_test_poly = np.vander(X_test, len(X_train))
# Finalmente calculamos error fuera de muestra
y_pred_test_model_1 = model_1.predict(X_test.reshape(-1, 1))
y_pred_test_model_2 = np.dot(X_test_poly, coeff)
print(f"Modelo 1: MSE: {mean_squared_error(y_test, y_pred_test_model_1)}")
print(f"Modelo 2: MSE: {mean_squared_error(y_test, y_pred_test_model_2)}")
Modelo 1: MSE: 3.0566262069391366
Modelo 2: MSE: 16400416.201402526
Observamos que el modelo lineal, tiene un error similar al error de entrenamiento (poca varianza), sin embargo, el modelo polinomial tiene un MSE gigantezco, lo que indica que es un mal modelo en este caso y no será capaz de hacer predicciones fuera de muestra con un rendimiento aceptable.
Conclusiones
- No hay receta para el éxito (dependiendo de la definición de éxito de la persona)
- Siempre es bueno desafiar tus propias creencias
- Se ilustraró un ejemplo de regresión lineal simple además de hacer una conexión con un estimador de máxima probabilidad.
- Se nombraron ciertas consideraciones prácticas al momento de aplicar regresión (teorema de Gauss-Markov)
- Se explicó una forma de interpretar resultados de regresión en bibliotecas tradicionales.
- Se repasó el concepto de sesgo y varianza en estimación de parámetros y su conexión con modelos predictivos.
- Se mostró un ejemplo didáctico de validación de modelos y las consecuencias del intercambio de sesgo y varianza.