Introducción

El propósito de esta serie es intentar desafiar las creencias del lector respecto a cómo ve la Inteligencia Artificial (IA). Llevo dos “episodios” explicando conceptos básicos de probabilidad. Por otro lado, el lector puede ir a artículos previos, donde explico los fundamentos de algunos modelos de IA:

Donde logramos entender, que generar una imagen nueva sigue el proceso de muestrar the una distribución de probabilidad $p(x)$ donde $x$ es una representación de la imagen. Los modelos generativos de lenguaje también se ven discutidos en los medios y redes sociales con frecuencia. Debemos entender sin embargo, que en esencia estos modelos también están muestreando de una distribución de probabilidad. Además, se debe recordar la definición de un modelo del lenguaje: Determinar si una oración pertenece o no al lenguaje. En la ciencia, se ha intentado hacer esto con diferentes enfoques, en un artículo previo por ejemplo, expliqué cómo implementar un simple modelo de lenguaje utilizando Cadenas de Markov: Un poco de NLP básico (no un tutorial de pytorch/tensor flow). En dicho artículo, también fuimos capaces de generar oraciones, simplemente haciendo un muestreo de una distribución de probabilidad $p(x)$, en este caso $x$ representa una oración.

Aún no he explicado todos los conceptos de variables aleatorias en la teoría de la probabilidad, y este artículo contendrá algunos conceptos, explicados de forma simple, para entender dos tópicos importantes: Covarianza y Correlación. Como bonus hablaré un poco sobre estimación de parámetros y test de hipótesis, en el sentido probabilístico.

Más tópicos sobre variables aleatorias

Covarianza y Correlación

Ahora introduciremos una medida cuantitativa de la fuerza y dirección de la relación entre dos variables aleatorias. Esta cuantificación tiene un rol fundamental en variados contextos, y será utilizada en la metodología de estimación que se explicará explicaré más adelante.

La covarianza de dos variables aleatorias $X$ e $Y$, denotada como $cov(X, Y)$, se define como:

$$cov(X, Y) = E\left[ (X - E[X])(Y - E[Y]) \right]$$

O alternativamente:

$$cov(X, Y) = E[XY] - E[X]E[Y]$$

Cuando $cov(X, Y) = 0$, decimos que $X$ e $Y$ no están correlacionadas. Puede observarse además que $cov(X, X) = var(X)$.

Consideremos el ejemplo del lanzamiento de dos dados de 4 caras. Para este ejemplo consideraremos las variables $X = max(a, b)$ e $Y = a + b$, donde $a$ y $b$ son los resultados del lanzamiento de cada dado. Las funciones de masa de probabilidad son:

$$ p_X(x)= \left\{ \begin{array}{ll} 1/16 & \mbox{si } x = 1 \\ 3/16 & \mbox{si } x = 2 \\ 5/16 & \mbox{si } x = 3 \\ 7/16 & \mbox{si } x = 4 \\ \end{array} \right.$$

$$ p_Y(y)= \left\{ \begin{array}{ll} 1/16 & \mbox{si } y = 2 \\ 2/16 & \mbox{si } y = 3 \\ 3/16 & \mbox{si } y = 4 \\ 4/16 & \mbox{si } y = 5 \\ 3/16 & \mbox{si } y = 6 \\ 2/16 & \mbox{si } y = 7 \\ 1/16 & \mbox{si } y = 8 \\ \end{array} \right.$$

Recordemos que para una variable aleatoria $X$ su esperanza se define como $\sum_x {xp_X(x)}$, de esta forma obtenemos:

$$E[X] = 1\cdot\frac{1}{16} + 2\cdot\frac{3}{16} + 3\cdot\frac{5}{16} + 4\cdot\frac{7}{16} = \frac{25}{8} = 3.125$$

$$E[Y] = 2\cdot\frac{1}{16} + 3\cdot\frac{2}{16} + 4\cdot\frac{3}{16} + 5\cdot\frac{4}{16} + 6\cdot\frac{3}{16} + 7\cdot\frac{2}{16} + 8\cdot\frac{1}{16} = 5$$

Finalmente, debemos calcular $E[XY]$, para ello, necesitamos la función de probabilidad de masa de $Z = XY$, para ello podemos dibujar la siguiente tabla:

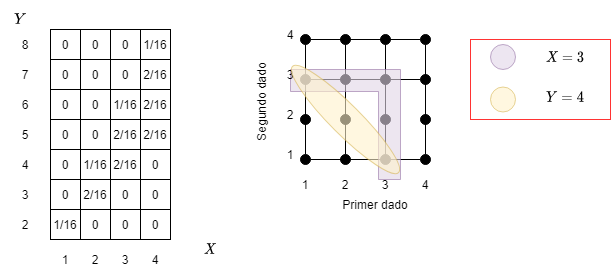
header

Fig 1: Ejemplo de probabilidad conjunta.

En la figura se ilustra la función de probabilidad de masa $p_Z$ de $Z = XY$, luego:

$$ \begin{align} E[XY] & = E[Z] \\ \sum_z {zp_Z(z)} & = 2\cdot\frac{1}{16} + 6\cdot\frac{2}{16} + 8\cdot\frac{1}{16} \\ & + 12\cdot\frac{2}{16} + 15\cdot\frac{2}{16} + 18\cdot\frac{1}{16} \\ & + 20\cdot\frac{2}{16} + 24\cdot\frac{2}{16} + 28\cdot\frac{3}{16} \\ & + 32\cdot\frac{1}{16} \\ & = \frac{135}{8} = 16.875 \end{align} $$

Finalmente, podemos obtener la covarianza:

$$cov(X, Y) = E[XY] - E[X]E[Y] = \frac{135}{8} - 5\cdot \frac{25}{8} = \frac{10}{8} = 1.25$$

Para ver de forma empírica esto, probemos implementar en python este experimento:

import numpy as np
import pandas as pd


def random_vars_two_dices(faces=4, exp=100000):
    """Experimento de lanzamiento de dos dados.

    :param faces: Número de caras de los dados, defaults to 4
    :type faces: int, optional
    :param exp: Cantidad de experimentos, defaults to 100000
    :type exp: int, optional
    :return: Dataframe con resultados de experimentos
    :rtype: pd.DataFrame
    """
    X = np.zeros(exp)
    Y = np.zeros(exp)

    for i in range(exp):
        dice1 = np.random.randint(1, faces + 1)
        dice2 = np.random.randint(1, faces + 1)
        X[i] = max(dice1, dice2)
        Y[i] = dice1 + dice2

    return pd.DataFrame({"X": X, "Y": Y})


# Sólo por reproducibilidad
np.random.seed(128)
df = random_vars_two_dices()

print(f"E[X] = {df['X'].mean()}")
print(f"E[Y] = {df['Y'].mean()}")
print(f"E[XY] = {(df['X']*df['Y']).mean()}")
print(f"cov(X, Y) = {df['X'].cov(df['Y'])}")

Asumiendo que no borraron la semilla configurada (si la borran deberían llegar a un resultado similar pero probablemente no igual), deberían ver lo siguiente:

E[X] = 3.12452
E[Y] = 4.99505
E[XY] = 16.85539
cov(X, Y) = 1.248268856688566

Si hacen una comparación de estos resultados, con los resultados teóricos, notarán que son extremadamente parecidos, y es lo esperable ya que conocemos la variable aleatoria y podemos calcular el valor de la esperanza y de la covarianza de forma exacta. En general en la práctica no se conocen los modelos probabilísticos de las variables en sí, pero si se pueden hacer ciertas estimaciones, si es que se tiene una muestra de datos representativa. Como ejercicio adicional, pueden calcular la covarianza de una variable binomial, por ejemplo considerando dos lanzamientos de monedas y X la cantidad de caras e Y la cantidad de sellos/cruces. Por ejemplo si consideran $n$ igual a 2, la covarianza debería darles -0.5 (esperable que estén negativamente correlacionadas, ya que mientras más caras menos cruces/sellos y viceversa).

El coeficiente de correlación $\rho(X, Y)$ entre dos variables aleatorias $X$ e $Y$ que tienen varianzas distintas de 0, se define como:

$$\rho(X, Y) = \frac{cov(X, Y)}{var(X)var(Y)}$$

Este coeficiente se puede ver como una versión normalizada de la covarianza $cov(X, Y)$, y de hecho, puede demostrarse que los valores de $\rho$ se encuentran entre -1 y 1. Si $\rho > 0$ (o $\rho < 0$), los valores de $X - E[X]$ e $Y - E[Y]$ “tienden” a tener el mismo (o opuesto, respectivamente) signo. El tamaño de $|\rho|$ provee una medida normalizada del grado de veracidad de esto. Básicamente la correlación nos permite comparar distintas variables (que pueden estar en diferentes escalas) y sus relaciones. Por completitud, calculemos la correlación de las variables $X$ e $Y$ consideradas en el experimento del lanzamiento de dos dados de 4 caras. Primero debemos calcular las varianzas:

$$ \begin{align} var(X) & = E\left[(X - E[X])^2\right] \\ & = \frac{1}{16}\left(1 - \frac{25}{8}\right)^2 + \frac{3}{16}\left(2 - \frac{25}{8}\right)^2 \\ & + \frac{5}{16}\left(3 - \frac{25}{8}\right)^2 + \frac{7}{16}\left(4 - \frac{25}{8}\right)^2 \\ & = \frac{55}{64} \end{align} $$

$$ \begin{align} var(Y) & = E\left[(Y - E[Y])^2\right] \\ & = \frac{1}{16}\left(2 - 5\right)^2 + \frac{1}{16}\left(2 - 5\right)^2 \\ & + \frac{2}{16}\left(3 - 5\right)^2 + \frac{3}{16}\left(4 - 5\right)^2 \\ & + \frac{4}{16}\left(5 - 5\right)^2 + \frac{3}{16}\left(6 - 5\right)^2 \\ & + \frac{2}{16}\left(7 - 5\right)^2 + \frac{1}{16}\left(8 - 5\right)^2 \\ & = \frac{5}{2} \end{align} $$

Finalmente:

$$\rho(X, Y) = \frac{\frac{5}{4}}{\sqrt{\frac{55}{64}\cdot\frac{5}{2}}} = \frac{\frac{5}{4}}{\sqrt{\frac{275}{128}}} \approx 0.8528$$

Para calcular la correlación entre las variables del ejemplo de los dados, pueden hacer df["X"].corr(df["Y"]) lo que entrega 0.8527042714104315 (básicamente el mismo valor obtenido teóricamente). Finalmente, podemos graficar la distribución conjunta de estas variables:

%matplotlib inline

import matplotlib.pyplot as plt
import seaborn as sns
from scipy import stats


plt.style.use("seaborn") # gráficos estilo seaborn
plt.rcParams["figure.figsize"] = (6,4) # Tamaño gráficos
plt.rcParams["figure.dpi"] = 200 # resolución gráficos
sns.jointplot(df["X"], df["Y"], kind="reg", stat_func=stats.pearsonr)

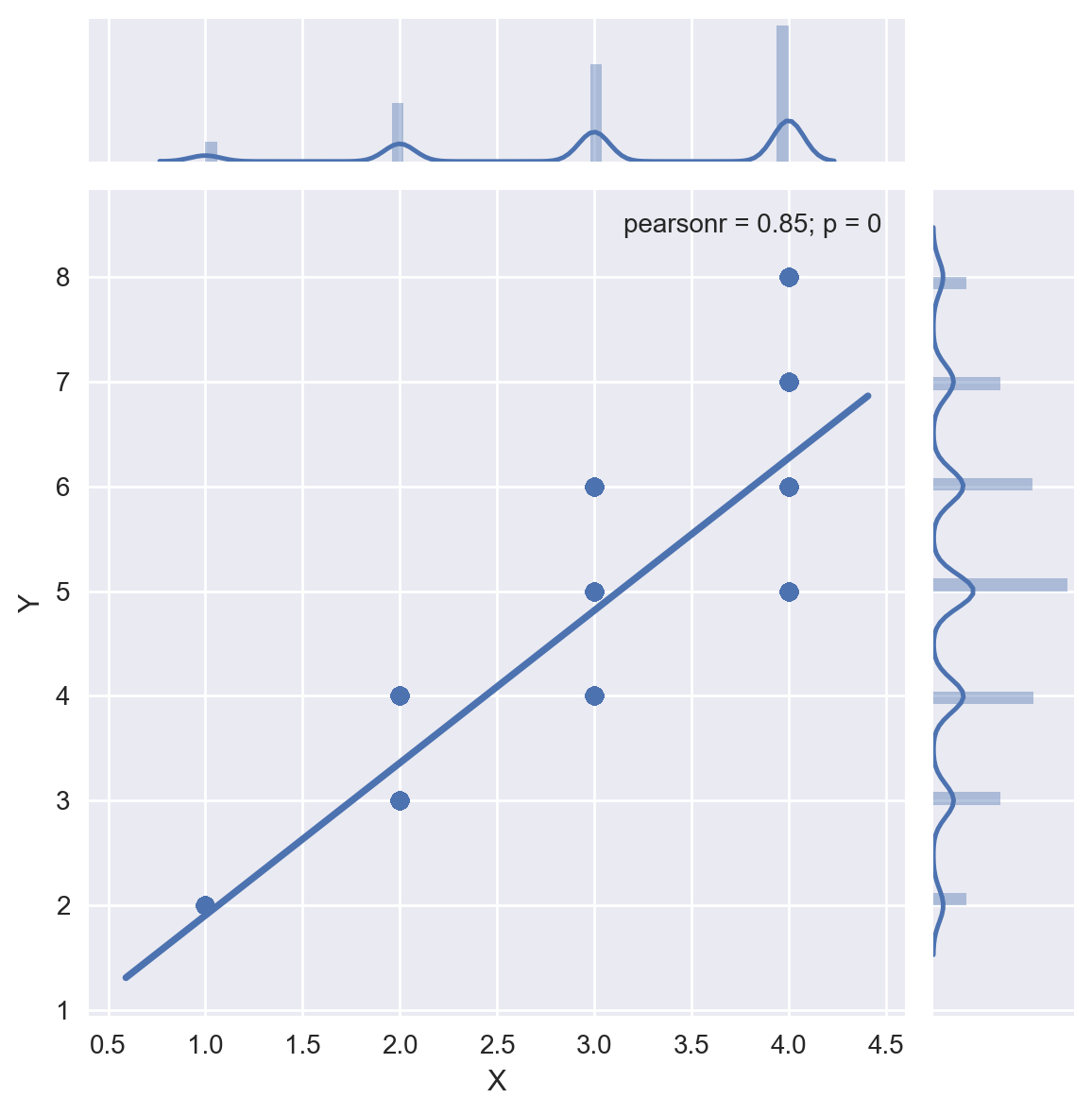
header

Fig 2: Gráfico de probabilidad conjunta ejemplo de los dados.

Se observa que las variables están correlacionadas positivamente y fuertemente (ya que el coeficiente de correlación es 0.85).

Inferencia Estadística Clásica

Como se mencionó algunas veces durante esta serie de artículos, existen dos visiones, frecuentista y Bayesiana. Para evitar complejizar las explicaciones, nos iremos por la visión clásica.

Tenemos una cantidad desconocida $\theta$ que queremos estimar, en el modelo clásico vemos a $\theta$ como un valor determinístico que desconocemos (contrario a la visión Bayesiana donde $\theta$ se le considera una variable aleatoria). Tenemos una observación $X$ aleatoria y cuya distribución $p_X(x;\theta)$ (o $f_X(x;\theta)$ si $X$ es continua) depende del valor de $\theta$. Por lo tanto, en esta visión se lidia de manera simultánea con múltiples modelos candidatos, un modelo por cada valor posible de $\theta$. En este contexto una “buena” forma de estimar $\theta$ es tener un proceso de estimación que posea ciertas propiedades deseables bajo cualquier modelo candidato.

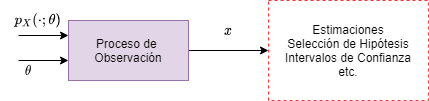
header

Fig 3: Proceso de inferencia.

Dadas las observaciones $X = (X_1, \ldots, X_n)$, un estimador es una variable aleatoria de la forma $\hat{\Theta} = g(X)$, para alguna función $g$. Notar que $X$ depende de $\theta$, lo mismo ocurre para la distribución de $\hat{\Theta}$. Se usa el término estimación para referirse a un valor actual calculado para $\hat{\Theta}$. Ahora introduciremos añguna terminología relacionada a varias propiedades de los estimadores:

El error de estimación, denotado $\tilde{\Theta}_n$ se define como $\tilde{\Theta}_n = \hat{\Theta}_n - \theta$ (notar que $n$ es el número de observaciones).
El sesgo (bias) del estimador, denotado por $b_{\theta}(\hat{\Theta}_n)$ es el valor esperado (esperanza) del error de estimación:

$$ \begin{equation} b_{\theta}(\hat{\Theta}_n) = E_{\theta}[\hat{\Theta}_n] - \theta \end{equation} $$

Decimos que $\tilde{\Theta}_n$ es imparcial (en algunos lados leerán insesgado, unbiased) si $E_{\theta}[\hat{\Theta}_n] = \theta$ para cualquier valor posible de $\theta$
Decimos que $\hat{\Theta}_n$ es asintóticamente imparcial si a medida que el número de observaciones $n$ aumenta, hay una convergencia de $E_{\theta}[\hat{\Theta}_n] = \theta$

Para entender de mejor manera los conceptos ilustrados hasta ahora, estimaremos dos parámetros importantes, el promedio y la varianza de una varible aleatoria. Supongamos que tenemos $n$ observaciones $X_1, \ldots, X_n$ i.i.d, que tienen un promedio común pero desconocido $\theta$ (promedio de la población). El estimador más natural de $\theta$ es el promedio muestral:

$$M_n = \frac{X_1 + \ldots + X_n}{n}$$

Calculemos la esperanza del error de estimación:

$$ \begin{array}{ll} E[M_n - \theta] & = E[M_n - \theta] \\ & = E[M_n] - \theta\\ & = 0 \\ \end{array} $$

Por lo tanto este estimador es imparcial, $E[M_n] = \theta$ (0 error de estimación). La varianza de este estimador:

$$ \begin{array}{ll} var(M_n) & = var\left( \frac{X_1 + \ldots + X_n}{n}\right) \\ & = \displaystyle \frac{1}{n^2} (var(X_1) + \ldots + var(X_2))\\ & = \displaystyle \frac{v}{n} \\ \end{array} $$

Donde $v$ es la varianza que comparten las muestras. Supongamos que ahora estamos interesados en un estimador de la varianza $v$ de la variable aleatoria a partir de las $n$ observaciones. Una opción natural sería:

$$\bar{S}_n^2 = \frac{1}{n} \sum_{i=1}^{n} (X_i - M_n)^2$$

Usando las siguientes relaciones (esperanza de $M_n$, esperanza de $X_i^2$, esto sale de $var(X) = E[X^2] - (E[X])^2$, y la esperanza de $M_n^2$ se obtuvo anteriormente):

$$E_{(\theta, v)}[M_n] = \theta, \quad E_{(\theta, v)}[X_i^2] = \theta^2 + v, \quad E_{(\theta, v)}[M_n^2] = \theta^2 + \frac{v}{n}$$

Luego resolviendo:

$$ \begin{array}{ll} E_{(\theta, v)}[\bar{S}_n^2] & = \displaystyle \frac{1}{n} E_{(\theta, v)} \left[ \sum_{i=1}^{n}{X_i^2 - 2M_nX_i + Mn^2} \right] \\ & = \displaystyle \frac{1}{n} E_{(\theta, v)} \left[ \sum_{i=1}^{n}{X_i^2} - 2M_n \sum_{i=1}^{n}{X_i} + \sum_{i=1}^{n}{Mn^2} \right] \\ & = \displaystyle \frac{1}{n} E_{(\theta, v)} \left[ \sum_{i=1}^{n}{X_i^2} - 2nM_n^2 + nM_n^2 \right] \\ & = E_{(\theta, v)} \left[ \frac{1}{n} \sum_{i=1}^{n}{X_i^2} - M_n^2 \right] \\ & = E_{(\theta, v)} \left[ \frac{1}{n} \sum_{i=1}^{n}{X_i^2}\right] - E_{(\theta, v)}\left[ M_n^2 \right] \\ & = \displaystyle \frac{1}{n} E_{(\theta, v)} \left[X_1^2 + \ldots + X_n^2\right] - (\theta^2 + \frac{v}{n}) \\ & = \displaystyle \frac{1}{n} n (\theta^2 + v) - (\theta^2 + \frac{v}{n}) \\ & = \displaystyle \frac{n - 1}{n} v \end{array} $$

Notamos que el estimador de la varianza definido como $\bar{S}_n^2$ no es imparcial, ya que su valor esperado no es $v$, pero a medida que el tamaño muestral aumenta ($n$), converge asintóticamente a la varianza real $v$. Si escalamos adecuadamente $\bar{S}_n^2$, obtenemos:

$$\hat{S}_n^2 = \frac{1}{n-1} \sum_{i=1}^{n} (X_i - M_n)^2 = \frac{n}{n - 1} \bar{S}_n^2$$

Del cual se puede demostrar que $E[\hat{S}_n^2] = v$, y este es un estimador imparcial de la varianza real $v$ para cualquier $n$. Sin embargo, si $n$ es lo suficientemente grande, entonces ambos estimadores son aproximadamente equivalentes (de aquí sale el $n - 1$ que hemos visto un par de veces).

Intervalos de Confianza

Supongamos que queremos ver si una moneda está cargada o no. Nos gustaría estimar el parámetro de probabilidad de que salga cara, por ejemplo. Sin embargo, comparar diferentes valores numéricamente hablando, no se podría diferenciar entre 0.4999 o 0.5, tampoco tendría sentido ya que es un estimado. En general, para esta situación nos interesa construir lo que se conoce como intervalo de confianza. En simples términos, este intervalo de confianza tiene una alta probabilidad de contener el parámetro que deseamos estimar, para cualquier valor del parámetro.

Para una definición más precisa, primero fijemos un nivel de confianza, $1 - \alpha$ donde $\alpha$ es típicamente un valor pequeño. Luego reemplazamos el estimador $\hat{\Theta}_n$ por un límite inferior $\hat{\Theta}_n^{-}$ y superior $\hat{\Theta}_n^{+}$, diseñados de manera que $\hat{\Theta}_n^{-} \leq \hat{\Theta}_n^{+}$, y:

$$P_{\theta}(\hat{\Theta}_n^{-} \leq \theta \leq \hat{\Theta}_n^{+}) \geq 1 - \alpha$$

En otras palabras, la probabilidad de que el intervalo contenga al parámetro a estimar, sea mayor que un cierto nivel de confianza. Notamos que $\hat{\Theta}_n^{-}$ y $\hat{\Theta}_n^{+}$ son función de las observaciones y por tanto, variables aleatorias cuya distribución dependen de $\theta$. Llamamos al intervalo $[\hat{\Theta}_n^{-}, \hat{\Theta}_n^{+}]$ intervalo de confianza.

En general los intervalos de confianza se construyen alrededor de un estimador $\hat{\Theta}_n$. Más aún, de una gran variedad de intervalos de confianza posibles, uno con un ancho pequeño es usualmente deseable. Sin embargo, esta construcción es complicada a veces debido que la distribución del error $\hat{\Theta}_n - \theta$ es desconocida o depende de $\theta$. Afortunadamente, para muchos modelos importantes $\hat{\Theta}_n - \theta$ es asintóticamente normal e imparcial. Con ello, queremos decir que la distribución de probabilidad acumulada de la variable aleatoria:

$$\frac{\hat{\Theta}_n - \theta}{\sqrt{var_{\theta}(\hat{\Theta}_n)}}$$

Se acerca a la distribución de probabilidad acumulada de una variable aleatoria normal estándar, a medida que $n$ aumenta, para cualquier valor de $\theta$. Ahora en casos en que la muestra no es de gran tamaño, para estimar la probabilidad, deberán usar la distribución del estudiante (la distribución t).

Test de Hipótesis Binario

En esta sección, nos enfocamos en describir el problema de elegir dos hipótesis. En el lenguaje estadístico tradicional, se consideran hipótesis $H_0$ (hipótesis nula) y $H_1$ (hipótesis alternativa). En esta configuración, $H_0$ toma el rol de modelo por defecto, que se demuestra o no refuta en base a los datos disponibles. Básicamente, el espacio de observaciones del vector de observaciones $X = (X_1, X_2, \ldots, X_n)$, se particiona en dos subconjuntos: un conjunto $R$, llamado región de rechazo, y su complemento, $R^C$, llamado región de aceptación. La hipótesis $H_0$ se rechaza (se dice falsa) cuando los datos observados caen en la región de rechazo $R$ y se acepta (se dice verdadera) en caso contrario.

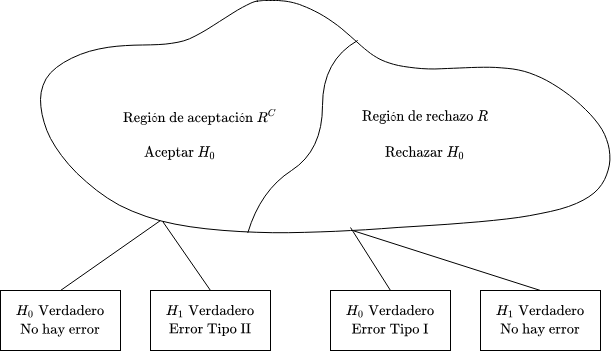
header

Fig 4: Test de Hipótesis Binario.

Dependiendo de la elección de la región de rechazo $R$, existen dos tipos posibles de error:

Rechazar $H_0$ siendo esta verdadera. Esto se conoce como error tipo I, o falso positivo, y ocurre con probabilidad:

$$\alpha(R) = P(X \in R; H_0)$$

Aceptar $H_0$ cuando es falsa. Esto se conoce como error tipo II, o falso negativo, y ocurre con probabilidad:

$$\beta(R) = P(X \notin R; H_1)$$

Test de Significancia

En test de hipótesis en entornos encontrados en la práctica no involucran siempre dos alternativas bien definidas, de modo que lo explicado en el apartado anterior (que involucra tener definida la hipótesis) no puede aplicarse. El propósito de este último apartado es introducir un enfoque a esta clase más general problemas. Sin embargo, se debe tomar la precaución, que una metodología única o universal no existe, y que existe un elemento significativo de juicio y “arte” que entra en el juego.

Consideremos el siguiente ejemplo: ¿Es mi moneda equitativa?

Una moneda se lanza independientemente $n = 1000$ veces. Sea $\theta$ la probabilidad de que salga cara en cada lanzamiento (desconocida). El conjunto de todos los posibles parámetros es $M = [0, 1]$. La hipótesis nula es $H_0$ (“la moneda es equitativa”) es $\theta = 1/2$. La hipótesis alternativa $H_1$ es $\theta \neq 1/2$.

En este caso, los datos observados son una secuencia $X_1, \ldots, X_n$, donde $X_i$ es 1 o 0 dependiendo si el lanzamiento $i$ fue cara o no. Supongamos que decidimos abordar el problema considerando el valor $S = X_1 + \ldots X_n$, el número de caras observadas y usando una regla de decisión de la forma:

$$\text{rechazar } H_0 \text{ si } \left|S - \frac{n}{2}\right| > \xi$$

Donde $\xi$ es un valor crítico adecuado que deberá ser determinado. Hasta ahora hemos definido la forma de la región de rechazo $R$ (el conjunto de datos que llevará a rechazar la hipótesis nula). Finalmente, escogemos el valor crítico $\xi$ de manera de que la probabilidad de falsos positivos es igual a un cierto valor $\alpha$:

$$P(\text{rechazar } H_0;H_0) = \alpha$$

Típicamente este $\alpha$ llamado nivel de significancia, es un número pequeño; En este ejemplo consideraremos $\alpha = 0.05$.

Ahora, para determinar el valor de $\xi$, necesitamos llevar a cabo algunos cálculos probabilísticos. Bajo la hipótesis nula, la variable aleatoria $S$ es binomial con parámetros $n = 1000$ y $p = 1/2$. Usando una aproximación normal a la binomial, y considerando $\alpha = 0.05:$ $$\left|S - \frac{n}{2}\right| > 1.96\cdot \sqrt{np(1 - p)}$$

De donde obtenemos que $\xi = 31$ es una elección apropiada. Ahora, si por ejemplo observamos un valor de $S$, $s = 472$, tendríamos:

$$|472 - 500| = 28 \leq 31$$

y la hipótesis $H_0$ no se podría rechazar al nivel de significancia del 5%.

Aquí se utiliza el vocabulario “no rechazada” en lugar de “aceptada” de forma deliberada. La razón es que no tenemos ninguna forma de asegurar que el valor del parámetro es 1/2 en lugar de, por ejemplo, 0.51. Lo único que podemos asegurar es que los datos observados de $S$ no entregan evidencia sustancial en contra de la hipótesis $H_0$.

Una metodología para realizar tests de significancia sobre una hipótesis $H_0$, basándose en observaciones $X_1, \ldots, X_n$:

Los siguientes pasos se realizan antes de observar los datos:
1. Elegir una estadística $S$, esto es, una variable aleatoria (escalar) que resumirá los datos a obtener.
2. Determinar la forma de la región de rechazo especificando el conjunto de valores de $S$ para el cual la hipótesis $H_0$ será rechazada en función de un valor crítico $\xi$ (aún a ser determinado).
3. Escoger un nivel de significancia, es decir, la probabilidad $\alpha$ de rechazar $H_0$ cuando era verdadera.
4. Elegir un valor de $\xi$ de manera que la probabilidad de un rechazo falso sea igual o aproximadamente igual a $\alpha$
Una vez que los valores $x_1, \ldots, x_n$ de $X_1, \ldots, X_n$ se obtengan:
1. Calcular el valor $s = h(x_1, \ldots, x_n)$ de la estadística $S$
2. Rechazar la hipótesis $H_0$ si $s$ pertenece a la región de rechazo.

Para cerrar esta sección, realizaremos un ejemplo un poco más concreto sobre test de significancia, sólo para tener más clara la intuición respecto a qué es lo que se “prueba”, y cómo funciona la metodología a grandes rasgos.

Cierto instructor del curso de No hago cursos pero es un ejemplo está interesado en conocer la diferencia de los puntajes finales del curso considerando dos generaciones diferentes. Los alumnos que se inscribieron en el curso fueron asignados a las generaciones de forma aleatoria, y el puntaje final se calculó en base a un conjunto de desafíos y pruebas estandarizadas para ambas generaciones. Se tomó una muestra de 8 estudiantes de la generación X y de 9 estudiantes de la generación 18. ¿Hay alguna diferencia entre las generaciones en los resultados logrados?

Generación X	Generación 18
35	52
51	87
66	76
42	62
37	81
46	71
60	55
55	67
53

Primer paso, se debe enunciar claramente cuáles van a ser las hipótesis (nula y alternativa). En este caso, la hipótesis nula será que no hay diferencia entre promedios de puntajes entre las generaciones.

$$H_0: \mu_1 = \mu_2$$

$$H_1: \mu_1 \neq \mu_2$$

El segundo paso identificar región de rechazo y el nivel de significancia. Ya que los alumnos fueron asignados aleatoriamente, y asumiremos que no se cambiaron de generación entre medio (independencia), asumiremos que los puntajes entre estudiantes son independientes (asumiremos que no se copiaron en la prueba jeje). Nos dicen que debemos considerar un nivel de significancia de $\alpha = 0.05$.

Paso 3, analizar los datos y calcular las estadísticas. Como el tamaño de la muestra es pequeño, no conviene usar una distribución normal. En este caso, utilizaremos la distribución del estudiante.

import numpy as np
from scipy import stats


# Muestras de ejemplo
gen_x = np.array([35, 51, 66, 42, 37, 46, 60, 55, 53])
gen_18 = np.array([52, 87, 76, 62, 81, 71, 55, 67])

# test-t de muestras independientes
stats.ttest_ind(gen_x, gen_18)

Ttest_indResult(statistic=-3.5334419686768466, pvalue=0.0030097571416081836)

El paso final es concluir acerca de los resultados. Como el valor de p es menor que el nivel de significancia establecido, esto significa que nuestro valor calculado cae en la región de rechazo de la hipótesis nula, por lo tanto, en base a los datos, rechazamos la hipótesis nula. Finalmente, concluimos que los dos grupos de estudiantes difieren significativamente en sus puntajes finales. Por lo tanto, podemos concluir plausiblemente que la diferencia de los puntajes se podría deber a la asignación (si estudiante fue asignado a generación X o a la 18).

Observación relevante: Este test es un poco obsoleto, antiguamente se hacía con una tabla y con ella se calculaban los valores de probabilidad. Sin embargo, con el desarrollo computacional, hoy en día tenemos mejores alternativas (ej. Test de Wilcoxon.)

Reflexiones Finales

Se explicaron los conceptos como covarianza y correlación para variables aleatorias
Se explicó la estimación de parámetros en la visión clásica
Se explicó en qué consisten los intervalos de confianza
Se explicó lo que es un test de hipótesis binario
Se trabajó un ejemplo de significancia estadística

Finalmente, siento que teniendo estos conceptos claros, se puede abrir esta caja mágica que hoy en día es la IA. Si bien, no tengo una fórmula para digerir los conocimientos de forma instantánea, en mi opinión para entender los conceptos y cómo funciona el mundo en temas científicos, es importante meter mano y darse la lata de escribir/simular/digerir los conceptos. Este proceso de digestión es lento, y no puede saltarse. No se puede llegar a ser experto en un tema de la noche a la mañana, hay un camino que es difuso, que puede ser largo; por lo que sigo sin entender, cómo estos influencers se saltan todo el trabajo requerido y comienzan a divulgar información errónea y sin bases ni fundamentos. Si llegaste hasta aquí, te recomiendo desafiar tu visión del mundo y empezar a tener un pensamiento crítico y hacerte responsable de tus debilidades y trabajarlas. Yo estoy en constante trabajo y a veces no avanzo, incluso retrocedo y vuelvo a lo básico. Sin embargo, la consistencia lleva a entender mejor estos temas y desarrollar un pensamiento crítico.